임의의 원형 경로 만들기
04 Dec 2018 • 0 Comments
도입
2주 전, 사각형 Grid 에서 임의의 겹치지 않는 원형 경로를 구해야 하는 업무가 생겼습니다. 요구 조건은 다음과 같았습니다.
- 순환 경로 (처음 == 끝)
- 중복되지 않는 깨끗한 1픽셀의 line으로 이어질 것 (가급적 상하좌우로만)
- 약간의 랜덤성
문제 정의에 따라서 A* 같은 탐색 알고리즘을 써서 구할 수도 있겠습니다만, 이때는 좀 쉽고 procedural 한 방법으로 풀어보고 싶다는 생각이 들었습니다. 고민 끝에 만든 방법은 다음과 같습니다.
- 랜덤한 원형 영역 구하기
- Cellular Automata 를 통해 영역 가장자리를 깨끗하게 만들고 외곽선만 남기기
- 시작점과 끝점을 select 하고, DFS 로 경로 찾기
완성된 경로는 다음과 같습니다. (파란색=시작점)
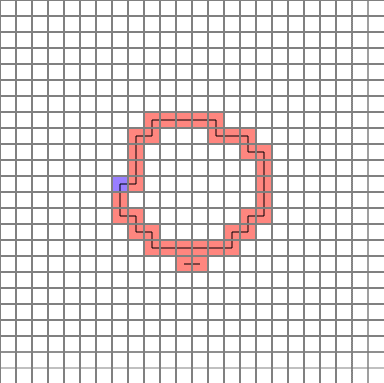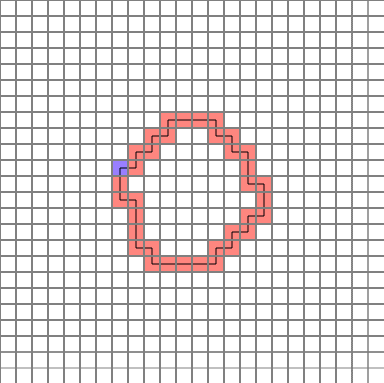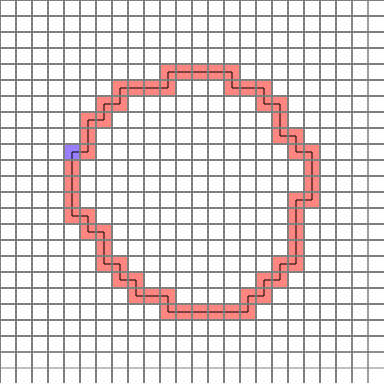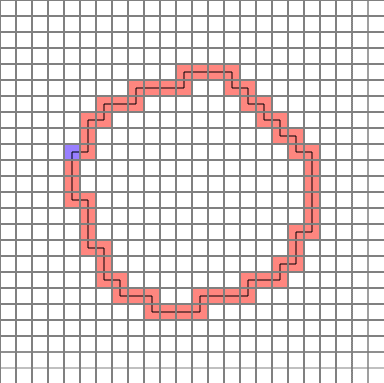
그럼 하나씩 분석해 보겠습니다.
랜덤한 원형 영역 구하기
위의 gif 파일을 보시면 알 수 있듯이 경로는 전체적으로 원형이지만 완벽한 원은 아닙니다. 약간 deform 된 원을 어떻게 표현할까 고민하다가 아주 옛날(10년 전쯤?)에 봤던 flash 파일이 하나 떠올랐습니다. 원주율(\(\pi\)) 값을 알아내기 위해서 몬테카를로 방식을 이용해서 사분원에 점을 찍어보는 것입니다. 이 때 원의 반지름을 r 이라고 할 때, 아래와 같은 식으로 \(\pi\) 값을 구할 수 있습니다.
\[\frac{사분원\phantom{0}안에\phantom{0}들어간\phantom{0}점의\phantom{0}개수}{전체\phantom{0}점의\phantom{0}개수} \simeq \frac{\frac{\pi r^2}{4}}{r^2} = \frac{\pi}{4}\]원본은 찾을 수가 없어서 비슷한 방법으로 원의 영역을 구해보는 youtube 영상의 링크를 추가해놓습니다.
그렇다면 이 아이디어처럼, 원형 영역을 구할 때 원의 영역과 겹치는 각 cell 에 일정한 개수의 점을 찍어서, 해당 점들이 원에 속하는 개수만큼 확률값을 부여해서 최종적으로 해당 cell 이 영역에 속하는지를 판단할 수 있지 않을까? 라고 생각했습니다. 원래 원에 포함되는 cell 은 무조건 100% 확률로 영역에 속하겠지만, 가장자리에 걸치는 cell 은 실행할 때마다 결과값이 달라집니다.
하지만 이대로는 삐죽하게 튀어나온 cell 들이 너무 많이 보입니다. Cellular Automata 는 이렇게 튀어나온 가장자리를 부드럽게 바꿔줄 수 있는 단순하면서도 강력한 PCG 기법입니다.
Cellular Automata 를 통해 영역 가장자리를 깨끗하게 만들고 외곽선만 남기기
Cellular Automata 는 cell 로 구성된 grid 에서 각 cell 이 일정한 상태(states)를 가진다고 할 때, 특정 규칙에 따라 그 상태를 바꿔주는 알고리즘입니다.
여기서는 일단 각 cell 의 8방향에 대해서 이웃(neighbor)의 수를 검사한 뒤에, 이웃이 3개 이하인 경우 해당 cell 을 없애줍니다. 이 과정을 5번 반복합니다. 보통은 2번 정도면 더 지울 cell 이 없어집니다.
그 다음 외곽선만 남기기 위해서, 각 cell 의 8방향에 대해서 이웃의 수가 8인 cell 을 지워줍니다. 이렇게 원의 안쪽에 있는 cell 을 없앨 수 있습니다.
이제 좀 그럴듯한 모습이 된 것 같습니다.
시작점과 끝점을 select 하고, DFS 로 경로 찾기
하지만 아직 문제는 남아 있습니다. 원형의 순환 경로를 찾기 위해서는 시작점을 잘 선택해야 합니다. 시작점은 가급적 이웃이 적은 cell 이어야 중복 경로가 형성될 가능성이 적어집니다. 이웃이 3개 이하인 cell 중에서 시작점을 정했고, 끝점은 시작점과 동일한 위치로 지정할 수도 있지만 알고리즘의 편의를 위해서 시작점의 상하좌우 중에 이웃하는 cell 로 정했습니다.
(시작점을 정할 때 랜덤한 위치가 아니라 순차적으로 cell 을 검사하기 때문에 위치가 비교적 일정합니다. 어차피 순환 경로를 만들 것이기 때문에 큰 문제는 되지 않습니다)
그럼 이제 경로를 DFS 로 찾으면 됩니다. stack 배열에 cell 을 하나씩 넣었다가 빼면서 끝점인지 여부를 검사합니다. 끝점이 아니라면 이웃을 찾아서 이웃에 방문한 적이 없으면 stack 에 넣습니다.
이제 완성입니다. 그림 파일은 위에서 보신 것과 동일합니다.
markdown 을 사용해서 블로그를 써보는 게 처음인데 생각보다 재밌습니다. 블로그를 개장했으니 열심히 공부하며 열심히 써야겠습니다.