Linkedin의 Queens 게임 맵 만들기

• 도입
• N-queen 문제
• Queens 문제의 대각선 배치 조건
• Queens 문제의 영역 조건
• 마치며

image link

도입

링크드인(Linkedin)은 전세계 10억 명 이상의 회원을 보유한 구인 구직 사이트로, 주간 방문자 수(WAU)는 6천 5백만 명에 달합니다.¹ SNS이지만 인스타그램이나 틱톡과는 달리 커리어, 업무 등 진지한 이야기가 많이 올라오는 곳이었는데요. 최근(2024년 5월 1일)에, 링크드인에 이런 분위기와 맞지 않게 게임 3종이 추가되어 이슈가 되었습니다.

그런데 생각해보면 가볍게 플레이할 수 있는 게임을 추가하는 것은 먼 옛날부터 페이스북 같은 SNS에서도 해왔던 일이고, 뉴욕 타임즈에도 십자말풀이(crossword)를 비롯해서 여러 개의 게임이 올라와 있습니다. 2021년에 만들어져서 선풍적인 인기를 끌었던 워들(Wordle)을 뉴욕 타임즈가 높은 가격에 인수²한 건 업계에서는 매우 유명한 사건이었습니다.

링크드인에서도 가볍게 플레이할 수 있는 게임의 중요성을 알았는지, 이번에 추가한 세 개의 게임은 모두 플레이하는 데에 5~10분이 걸릴 정도로 짧습니다. 이 중 두 개의 게임은 언어와 관련된 것이기 때문에 알고리즘 적으로 생성하는 것은 간단치 않아 보이고(물론 LLM을 사용하면 금방 할 수도 있겠지만 여기서는 다루지 않겠습니다), 이 블로그에서는 Queens라는 게임의 맵을 생성하는 방법에 대해서 다뤄보도록 하겠습니다.

N-queen 문제

Queens 게임을 이해하려면 먼저 N-queen 문제를 알아야 합니다. NxN의 보드에 N개의 퀸을 서로 공격하지 않는 위치에 놓아야 하는 N-queen 문제는 무차별 대입 방식으로 풀기에는 매우 시간이 오래 걸리지만, 문제를 풀기 위한 조건을 조금만 수정해서 접근하면 비교적 쉽게 풀 수 있는 유명한 알고리즘 문제입니다.

4-queen 문제 해답의 예시

체스에서 퀸은 현재 위치에서 같은 행, 같은 열, 대각선의 모든 칸으로 움직일 수 있으므로, 서로 공격하지 않기 위해서는 퀸끼리 서로 행, 열, 대각선으로 겹치지 않는지 검사해야 합니다.

문제를 약간 단순화해서, 퀸이 아닌 룩(Rook)이라고 해보면 어떨까요? 룩은 현재 위치에서 같은 행, 같은 열로 움직일 수 있지만 대각선으로는 움직일 수 없습니다.

4-rook 문제 해답의 예시. 룩은 각각 0번, 1번, 2번, 3번 행&열에 배치되어 있습니다.

N-queen과 N-rook의 답에서 볼 수 있는 공통점은, 퀸과 룩을 같은 행, 같은 열에 두 개 이상 놓을 수는 없다는 것입니다. 룩을 한 행에 하나씩 순차적으로 배치할 때, 각 룩이 서로 다른 열에 있기만 하다면 N-rook 문제의 정답이 됩니다.

코드 1. N-rook 문제의 정답을 구하는 코드

  위 코드에서 search(arr) 함수는 빈 배열로 시작해서 각 행에 배치되어야 할 룩의 열(column) 번호를 하나씩 찾아나갑니다. search(arr) 함수의 종료 조건은 19행에서 볼 수 있듯이 arr 의 길이가 N 과 동일할 때이고, 그렇지 않다면 0부터 N-1까지의 숫자 중에서 현재 arr 에 없는 숫자 i 가 있다면 찾아서 새로운 search([...arr, i]) 함수를 호출합니다. 우측의 결과 창에서는 지면상 모든 결과를 표시하지는 않지만, N=4일 때의 풀이 수는 24인 것을 확인할 수 있습니다. 30행의 N을 5, 6, 8 등으로 바꿔보면, 이 숫자는 수학에서 배우는 팩토리얼과 같다는 것을 알 수 있습니다. 즉 N-rook 문제의 답 개수는 \(N!\) 입니다.

그럼 N-queen 문제는 어떻게 풀어야 할까요? 위의 코드에서 search 함수를 살짝 바꿔서, 대각선 조건을 체크하면 됩니다. search 함수의 매개변수인 arr 에, 새로 추가될 숫자인 i와 대각선으로 겹치는 퀸이 있는지를 체크하는 것입니다. 코드로 표현하면 아래와 같습니다.

코드 2. N-queen 문제의 정답을 구하는 코드

  24행의 if 문 뒤에 추가된 조건은 arr.filter((c,idx) => Math.abs(i-c) == Math.abs(arr.length-idx)).length == 0 으로, 현재 arr 에 있는 퀸 중에 arr.length 번째 행, i 번째 열에 배치될 퀸과 열의 차이(Math.abs(i-c))와 행의 차이(Math.abs(arr.length-idx))가 동일한 원소가 없는지를 체크하는 것입니다. 만약 없다면 배치가 가능하므로 i 를 arr 에 추가한 search([...arr, i]) 함수를 호출합니다. N=4일 때의 답은 2개로 줄어들었습니다. 30행에서 N을 8로 바꿔보면 답이 92로 나오는 것을 확인할 수 있습니다. N-rook 문제보다는 정답의 개수가 꽤 적어졌습니다.

N=8일 때의 첫번째 해답인 0, 4, 7, 5, 2, 6, 1, 3번째 열에 각각 퀸을 배치한 모습

Queens 문제의 대각선 배치 조건

그런데 Queens 문제의 대각선 배치 조건은 N-queen 문제와는 약간 다릅니다. 모든 행, 모든 열에 하나의 퀸만 배치되어야 하는 조건은 같으나, 대각선으로는 두 퀸이 서로 인접하지만 않으면 됩니다. 즉 대각선으로 한 칸 떨어져 있지만 않으면 괜찮은 것입니다.

코드 3. Queens 게임 중 퀸 배치의 정답을 구하는 코드

24번째 행의 if 조건은 arr 에 있던 퀸 전체를 체크하는 것에서, 마지막 퀸(arr[arr.length-1])을 체크하는 것으로 바뀌었습니다. 각 행에 순차적으로 퀸을 배치하기 때문에, 예를 들어 3번째 행에 퀸을 배치한다면 1번째 행의 퀸은 신경쓸 필요가 없고, 2번째 행의 퀸만 신경쓰면 됩니다. 이렇게 했을 때 N=8에서의 정답 개수는 5,242개가 됩니다. 기존 N-queen보다는 증가한 양입니다.

N=8일 때의 첫번째 해답인 0, 2, 4, 1, 5, 7, 3, 6번째 열에 각각 퀸을 배치한 모습

Queens 문제의 영역 조건

그런데 Queens 문제는 여기서 한 걸음 더 나아갑니다. 각 퀸은 위의 조건에 더해서, 같은 색깔을 가진 영역에 하나씩만 놓여야 하는 것입니다. 예를 들어 위에서 살펴본 02415736 열에 퀸을 배치한 모습은, 영역 조건을 추가해서 아래와 같이 표시할 수 있습니다.

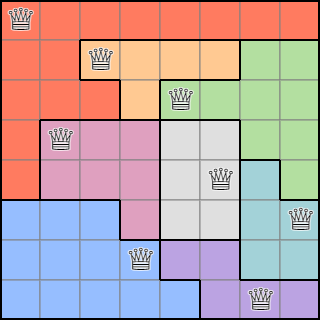8x8 체스판을 8개의 영역으로 나누고 각 영역에 1개의 퀸만 배치되도록 한 모습

이때 영역은 서로 연결되어 있어야 하고, 하나의 칸은 하나의 영역에만 속해야 하고, 모든 칸은 각기 하나의 영역에 속해야 한다는 전제조건이 암시적으로 적용되는 것 같습니다. Linkedin Queens 게임에서 서비스하는 게임은 N=8일 경우이고, 이것을 위해 위에서 구한 5,242개의 퀸 배치 중 하나를 사용하고, 영역을 랜덤하게 지정하면 우리는 Linkedin Queens와 동일하게 보이는 맵을 얻을 수 있을 것입니다. 물론 재미가 있을지는 다른 문제이지만, 이 블로그에서는 그것까지 다루지는 않기로 하겠습니다.

영역 조건을 만족시키기 위해서, 코드 3의 퀸 배치 상태에서 시작합니다. 먼저 각 퀸이 배치된 칸을 서로 다른 영역으로 지정합니다.

체스판 중 퀸이 배치된 칸을 서로 다른 영역으로 지정한 모습

그 다음으로 각 영역의 상하좌우로 이웃인, 아직 영역이 지정되지 않은 영역을 후보로 지정합니다.

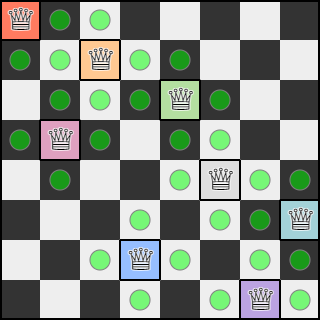지정된 후보 시각화

그 다음으로는 이 중 하나를 랜덤하게 골라서, 인접한 영역 중 하나에 속하도록 합니다. 그 후 후보 목록을 업데이트합니다.

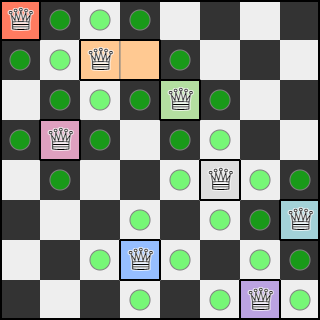1행 3열의 후보를 영역에 지정한 후, 후보 목록 업데이트

이 과정을 반복하면 퀸이 배치된 상태에서 랜덤한 영역 조건 맵을 얻을 수 있습니다.

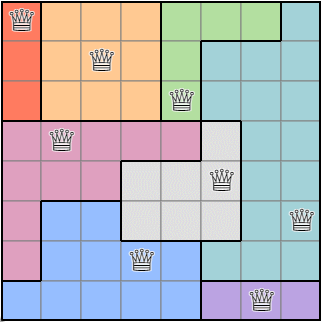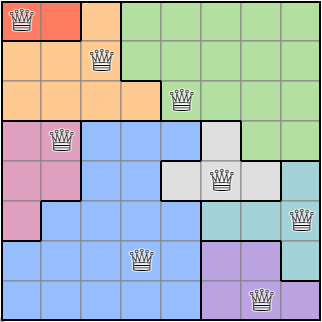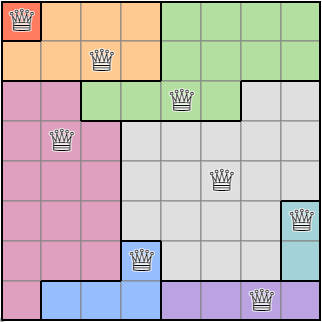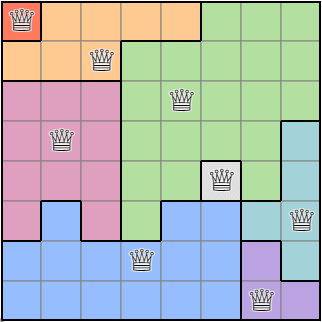영역 조건을 구하는 알고리즘의 실행 결과

마치며

이번 글에서는 링크드인에 추가된 Queens 게임의 맵을 만드는 방법을 살펴보았습니다. 이 밖에도 PCG로 게임 레벨을 만드는 방법에 대한 다양한 기고문을 생각하고 있으니 많은 관심 부탁드립니다. 추가로 궁금하신 사항은 문의해주시면 답변드리겠습니다. 긴 글 읽어주셔서 감사합니다.