강화학습 알아보기(1) - 가치 함수

10 Feb 2019 • 0 Comments Tags:

[ reinforcement-learning ]

강화학습이란?
이론적 배경
Grid World
가치 함수

강화학습이란?

2016년에 있었던 딥마인드의 알파고(AlphaGo)와 이세돌 9단의 대국은 인공지능이 세계 최초로 프로 최고수급의 인간을 바둑에서 이긴 사건으로 화제가 되었습니다. 2018년에는 5대 5로 팀을 나눠 싸우는 협동 게임인 DOTA2 에서 OpenAI 의 연구진이 정해진 영웅 조합으로 프로에 근접한 아마추어 팀을 이겼고, 2019년에는 딥마인드의 알파스타(AlphaStar)가 스타크래프트2에서 같은 종족전(Protoss)으로 프로 최고수를 이기는 경기를 선보였습니다. 이 놀라운 성과들은 인공지능의 한 갈래인 강화학습이 뒷받침하고 있습니다.

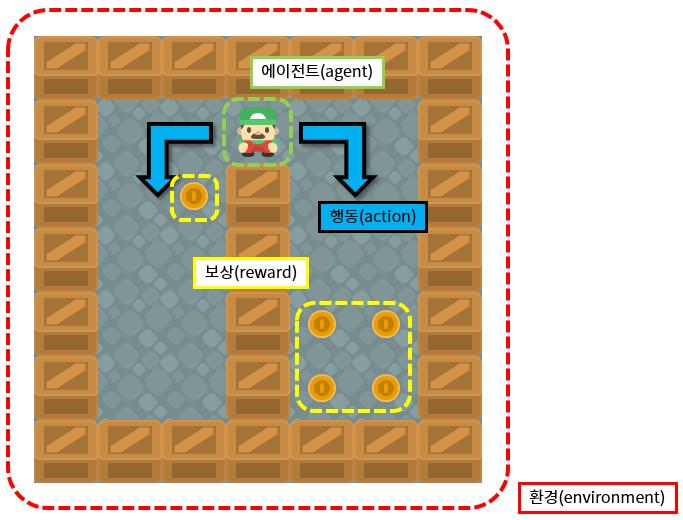
강화학습은 에이전트(agent)가 정해진 환경(environment) 속에서 현재의 상태(state)를 인식하고, 행동(action)을 통해 보상(reward)을 최대화하는 방향으로 학습하는 알고리즘입니다. 보상이 커지도록 하는 행동은 더 자주 하고, 보상을 줄이는 행동은 덜하게 됩니다.

이 과정에서 강화학습은 여러 번의 시도를 통해 실수를 하고, 그 실수를 교정하면서 점차 원하는 답을 찾아가게 됩니다. 단순화시켜서 말하면 일단 해보고, 점차 고쳐나가는 방법이라고 할 수 있습니다.

Sokoban Tileset by Kenney

이론적 배경

강화학습은 인간과 동물의 학습 방식에 큰 영향을 받았습니다.

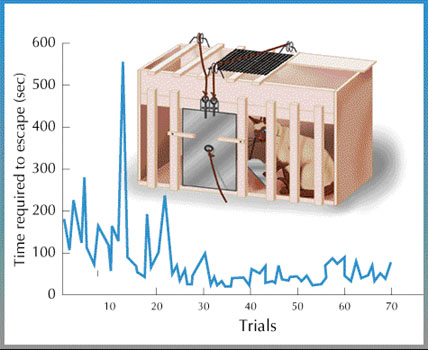
20세기 초 미국의 심리학자인 에드워드 손다이크(Edward Thorndike)는 고양이를 이용한 실험을 통해서 효과 법칙(Law of effect)이라는 것을 주장했습니다. 고양이를 상자 안에 넣은 다음 바깥에 생선을 놓고, 레버를 터치해야만 상자에서 빠져나갈 수 있게 하자, 갇히는 횟수가 반복될수록 고양이가 레버를 점점 빠르게 터치해서 상자에서 빨리 빠져나가게 되었습니다. 효과 법칙은 이렇게 만족(생선)을 주는 행동(레버 터치)이 강화(reinforce)된다는 이론입니다.

이미지 링크

딥마인드를 설립한 데미스 허사비스(Demis Hassabis)는 영국의 UCL 에서 인지신경과학 박사학위를 받았습니다. 인지신경과학은 인간의 뇌에서 일어나는 기억과 의사결정에 대한 학문으로, 인간의 행동을 이해하기 위한 학문입니다. 그는 2012년에 앨런 튜링 탄생 100주년을 맞아 Nature에 실린 특별 기고문에서 블랙박스로 간주되어 동작원리를 알 필요가 없었던 것으로 간주되었던 인간의 뇌의 동작 원리를 알고리즘 수준까지 이해해야 더 발전된 인공지능을 만들 수 있을 것이라고 주장했습니다.

강화학습의 선구자인 리차드 서튼(Richard Sutton)과 앤드류 바르토(Andrew Barto)는 강화학습의 초기부터 효과적인 모델이었던 시간차 학습 모델(Temporal difference model)을 동물의 학습 이론을 통해 설명했습니다. 시간차 학습 모델은 몬테카를로 모델과 더불어 가장 중요한 강화학습의 개념입니다. 이 두 가지에 대해서는 다음 글에서 차차 설명드리도록 하겠습니다.

Grid World

강화학습을 비롯한 인공지능에서는 오래 전부터 실제의 세계를 단순화시킨 Grid World 에서 문제를 풀어왔습니다. Grid World 는 2차원의 한정된 공간으로 격자(Grid) 위에 에이전트와 목표, 보상 등을 배치하고 다양한 알고리즘으로 문제를 풀어볼 수 있습니다.

let canvas = document.getElementById('editor_canvas_0');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Step(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];

button.onclick = function() {
    if (is_running) return;
    iterate(false);
}

button2.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let action = Math.floor(Math.random() * 4);
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 60);
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

여기에 Grid World 의 간단한 예시가 있습니다.¹ 붉은색 세모(🔺)는 에이전트를 나타내며, 파란색 원(🔵)은 에이전트가 도달해야 하는 목표를 나타냅니다.

여기서는 에이전트가 주어진 시간(step) 내에 목표와 같은 격자에 도달하면 성공으로, 한 번의 실행(episode)이 끝나고 다음 실행이 시작됩니다. 목표에 도달하기 위해서 에이전트는 매 step 마다 현재 위치와 맞닿아 있는 4개의 격자(상하좌우)중 하나로 이동하는 행동(action)을 할 수 있습니다. 격자의 끝에서는 움직임이 제한됩니다(격자가 없는 곳으로 이동불가).

목표에 도달하면 +1 의 보상을 주고, 빠르게 보상을 찾는 행동에 인센티브를 부여하기 위해서 매 step 마다 -0.1 의 보상(페널티)을 줍니다. 강화학습의 에이전트는 보상을 최대화하는 쪽으로 행동하고 반대되는 행동은 덜하려고 하기 때문에 이런 세팅이 필요한 것입니다.

일단 Step(random action) 버튼을 누르면 에이전트가 한번의 행동을 수행하고, Loop(random action) 버튼을 누르면 전체 Episode 가 100 이 될 때까지 자동으로 행동을 수행합니다. 매 step 마다 에이전트는 가능한 행동 중 하나를 랜덤하게 선택합니다. 아직은 강화학습이 아닙니다. 에이전트는 공기 중의 분자처럼 무작위로 움직일 뿐입니다. 그러다 운이 좋으면 목표에 도달하기도 하지만, 그렇지 못하고 동떨어진 곳에서 episode 가 끝날 때도 많습니다.

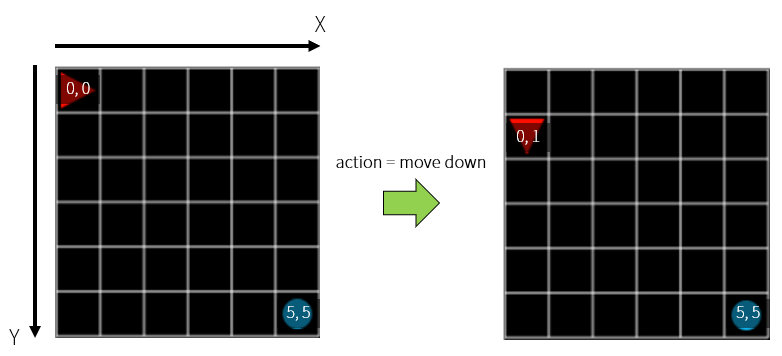
에이전트가 목표를 잘 찾게 하려면 먼저 목표가 어디에 있는지 알아야 합니다. 즉 환경에 대한 상태(state) 정보를 알아야 합니다. 현재 Grid World 는 6x6, 총 36 개의 격자로 구성되어 있습니다. 초기 상태(initial state)에서 첫번째 칸(x=0, y=0)에는 에이전트가 위치하고, 마지막 칸(x=5, y=5)에는 목표가 위치합니다. 여기서 아래쪽으로 이동하는 행동을 한다면, 에이전트의 위치는 (x=0, y=1) 이 될 것입니다.

위의 랜덤한 실행을 통해서 각 step 마다 reward 를 받고, 이것을 모두 합치면 최종 그래프에 표시되는 최종 reward 가 됩니다. 하나의 episode 를 예로 들어보겠습니다.

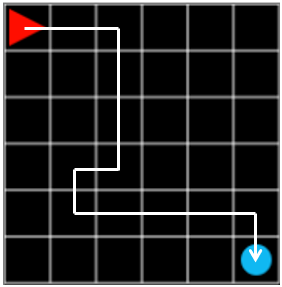그림 1. steps: 12, reward: -0.1

그림 1의 episode 에서 에이전트는 조금 헤매기는 했지만 목표를 찾는 데에 성공했습니다. 이때 최종 reward 는 각 step 마다 -0.1, 마지막에 목표에서 +1.0 을 받았기 때문에 \(-0.1 \times 11 + 1.0 = -0.1\) 이 됩니다.

이번 episode 에서 지나온 격자들을 저장하고 거기에 이번에 받은 reward 를 저장하면 어떨까요?

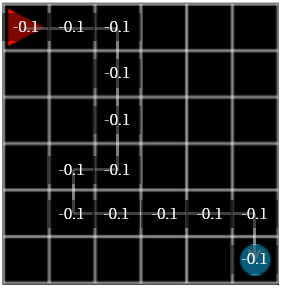그림 2

다음 행동에서 random action 이 아니라 격자들에 저장되어 있던 reward 를 참조하는 것입니다. 어느 격자로 움직일지 선택할 때는 reward 가 가장 큰 격자를 선택하고, 2개 이상이 같을 경우 그 중 하나를 랜덤하게 선택합니다. 그리고 초기의 reward 값은 모두 0 으로 저장합니다.

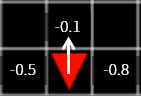그림 3. 가장 높은 reward 인 -0.1을 가진 격자로 움직입니다.

그리고 episode 를 반복하면서 격자가 가진 값을 업데이트 해줍니다. 어떻게 업데이트를 해야할까요? 1) 새로운 값으로 덮어씌우기, 2) 평균 취하기. 1번보다는 2번이 안정적으로 보입니다.

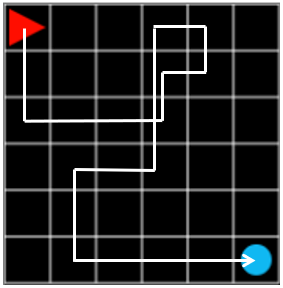그림 4. steps: 20, reward: -0.9

그림 4의 episode 에서 에이전트는 조금 더 헤매기는 했지만 목표를 찾는 데에 성공했습니다. 이때 최종 reward 는 각 step 마다 -0.1, 마지막에 목표에서 +1.0 을 받았기 때문에 \(-0.1 \times 19 + 1.0 = -0.9\) 가 됩니다.

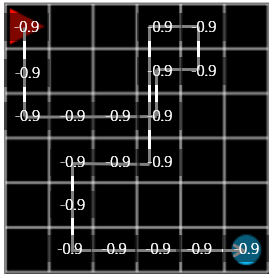그림 5

그러면 2의 방법대로 겹치는 격자에 대해서 reward 값의 평균을 내보면 그림 6과 같이 됩니다.

그림 6

그럼 이렇게 랜덤 행동에 의한 실행을 반복해서 각 격자의 reward 를 구하고, 이 reward 에 따라 에이전트를 행동시켜보겠습니다.

let canvas = document.getElementById('editor_canvas_1');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
env.maxEpisodes = 50;
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Run(by reward)';
button2.disabled = true;
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];
let value_array = new Array(env.grid_W * env.grid_W).fill(0);
let cnt_array = new Array(env.grid_W * env.grid_W).fill(0);
let stepped_array;

button.onclick = function() {
    if (is_running) return;

    is_running = true;
    stepped_array = [0];
    iterate(true);
}

button2.onclick = function() {
    iterate(true);
}

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    let max = Math.max(...value_array);
    let min = Math.min(...value_array);
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] / max * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor((1.1-Math.abs((value_array[i]-min) / (max-min+1e-4))) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function iterate(is_loop = true) {
    let action;
    if (button2.disabled) {
        action = Math.floor(Math.random() * 4);
    }
    else {
        let values = [];
        let x, y, idx;
        for (let i = 0; i < dirs.length; i += 1) {
            x = agent.x + dirs[i][0];
            y = agent.y + dirs[i][1];
            if (x >= 0 && x < env.width &&
                y >= 0 && y < env.height) {
                idx = x + y * env.grid_W;
                values.push(value_array[idx]);
            }
            else {
                values.push(-Number.MAX_VALUE);
            }
        }

        // find max values
        const m = Math.max(...values);
        values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
        action = values[Math.floor(Math.random() * values.length)];
    }
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();

    let idx = agent.x + agent.y * env.grid_W;
    if (stepped_array.indexOf(idx) === -1) {
        stepped_array.push(idx);
    }

    if (done || env.steps >= env.maxSteps) {
        let reward = Math.floor(agent.reward * 10) / 10;
        rewards_array.push(reward);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 60);
        }

        if (button2.disabled) {
            for (let i = 0; i < stepped_array.length; i += 1) {
                const idx = stepped_array[i];
                cnt_array[idx] += 1;
                value_array[idx] += (reward - value_array[idx]) / cnt_array[idx];
                value_array[idx] = Math.floor(value_array[idx] * 10) / 10;
            }

            stepped_array = [];
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
    else {
        if (button2.disabled) {
            button2.disabled = false;
            button.disabled = true;
            env.episodes = 0;
        }
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

Loop(random action) 버튼을 눌러서 50번의 episode 를 돌려본 다음, Run(by reward) 버튼을 눌러서 reward 에 따라 행동하는 에이전트를 관찰해봅니다. 그런데 에이전트는 목표를 잘 찾아가지 못합니다. 때로는 잘못된 목표에 빠져서 헤매다가 끝나는 경우도 있습니다.

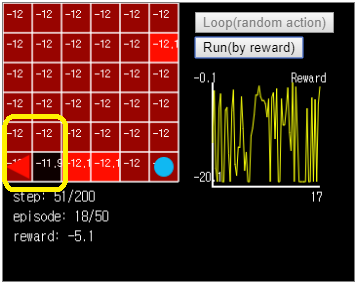그림 7. 이 경우 에이전트는 Grid World 좌하단에서 빠져나오지 못합니다.

문제의 원인 중 하나는 각 격자가 가지게 되는 reward 값이 거의 일정하다는 것입니다. 랜덤한 액션으로 움직이는 에이전트는 목표에 도달하기 전에 너무 많은 격자를 거치기 때문입니다. 그러면 이 중 쓸모있는 움직임, 즉 목표에 도달하는 행동에 기여도가 더 높은 움직임을 구별할 수 있을까요?

일단 문제를 거꾸로 생각해보겠습니다. 목표에 도달하기 바로 전인 (x=4, y=5) 에 에이전트가 위치할 때, 에이전트는 A, B, C 중 어디로 움직여야 할까요? 당연히 C 로 움직이는 것이 최적의 선택이 될 것입니다. C 로 움직이면 보상은 +1, A 나 B 로 움직이면 보상은 -0.1 이기 때문입니다.

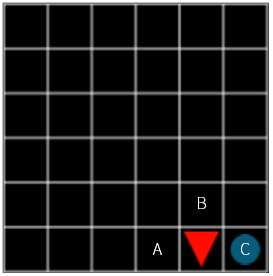그림 8

이때 C 의 가치(value)는 A, B 보다 높을 수밖에 없습니다. 그럼 여기서 한 칸 떨어져 있는 위치에서는 어떨까요? 여기서도 당연히 C 가 제일 최적의 선택일 것입니다. 당장 다음 step 에서 받는 보상은 A, B, C 모두 -0.1 로 동일합니다. 그럼에도 C 를 선택하는 이유는 목표에 제일 가까운 위치이기 때문입니다. 즉 C 를 선택하면 다음에 얻을 수 있는 보상이 A 와 B 를 선택했을 때보다 훨씬 클 가능성이 있기 때문입니다.

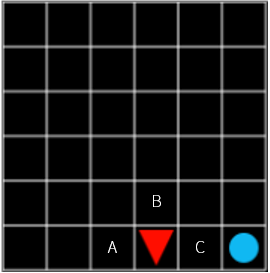그림 9

그런데 그림 8의 C 와 그림 9의 C 는 같은 가치를 가지고 있을까요? 이런 경우는 어떨까요?

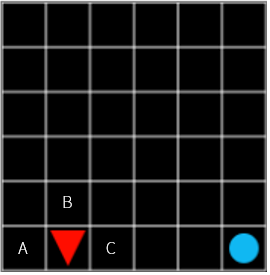그림 10

그림 10의 C 는 위의 그림 8, 9의 C 와 동일하게 높은 가치를 가지고 있을까요? 모든 것이 안정된 지금 예시의 Grid World 라면 그렇다고 말할 수도 있겠습니다. 하지만 step 을 진행할 때마다 일정 확률로 폭탄이 터진다면 어떨까요? 목표로 가는 길에 닿으면 -100 의 보상을 주는 방해 요소가 나타난다면? 그럼에도 C 로 가는 것이 일단 최적의 선택이기는 하지만, 바로 눈앞에 한 걸음만 내딛으면 보상이 있는 경우보다는 가치가 높다고 말할 수 없을 것 같습니다.

이런 경우를 설명하기 위해 감가율(discount rate)이 도입됩니다. 감가율이란 현재 받을 수 있는 보상이 미래에 받는 보상보다 가치가 높다는, 반대로 말하면 미래의 보상은 현재의 보상보다 가치가 낮다 는 것을 의미하는 개념입니다. 0.0~1.0 의 숫자로 표현되며, 보통 0.95, 0.99 등의 값이 쓰입니다. 수학식에서는 \(\gamma\)(감마) 라는 기호로 표현합니다.

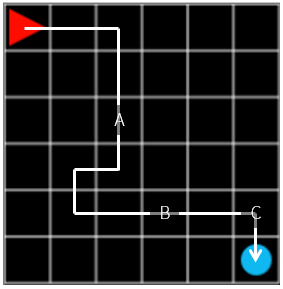그림 11. steps: 12, reward: -0.1

위에서 살펴본 감가율을 적용시켜본다면, 그림 11의 A, B, C 중에 기여도가 제일 높은 것은 C 일 것이고, 그 다음 B, A 순서일 것입니다. 최종 행동에서 떨어진 step 만큼 \(\gamma\) 를 곱해서 reward 를 계산한다면, 전체 보상이 -0.1 일 때 C 의 보상은 \(\gamma \times -0.1\), B 의 보상은 \(\gamma ^ 3 \times -0.1\), A 의 보상은 \(\gamma ^ 8 \times -0.1\) 이 됩니다.

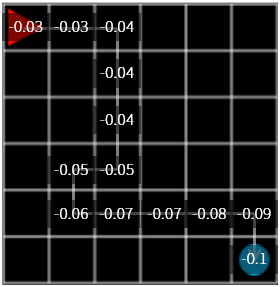그림 12. \(\gamma = 0.9\) 일 때의 reward 변화

let canvas = document.getElementById('editor_canvas_2');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
env.maxEpisodes = 50;
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Run(by reward)';
button2.disabled = true;
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];
let value_array = new Array(env.grid_W * env.grid_W).fill(0);
let cnt_array = new Array(env.grid_W * env.grid_W).fill(0);
let stepped_array;
const gamma = 0.9;

button.onclick = function() {
    if (is_running) return;

    is_running = true;
    stepped_array = [0];
    iterate(true);
}

button2.onclick = function() {
    iterate(true);
}

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    let max = Math.max(...value_array);
    let min = Math.min(...value_array);
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] / max * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor((1.1-Math.abs((value_array[i]-min) / (max-min+1e-4))) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function iterate(is_loop = true) {
    let action;
    if (button2.disabled) {
        action = Math.floor(Math.random() * 4);
    }
    else {
        let values = [];
        let x, y, idx;
        for (let i = 0; i < dirs.length; i += 1) {
            x = agent.x + dirs[i][0];
            y = agent.y + dirs[i][1];
            if (x >= 0 && x < env.width &&
                y >= 0 && y < env.height) {
                idx = x + y * env.grid_W;
                values.push(value_array[idx]);
            }
            else {
                values.push(-Number.MAX_VALUE);
            }
        }

        // find max values
        const m = Math.max(...values);
        values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
        action = values[Math.floor(Math.random() * values.length)];
    }
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();

    let idx = agent.x + agent.y * env.grid_W;
    if (stepped_array.indexOf(idx) === -1) {
        stepped_array.push(idx);
    }

    if (done || env.steps >= env.maxSteps) {
        let reward = Math.floor(agent.reward * 10) / 10;
        rewards_array.push(reward);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 60);
        }

        if (button2.disabled) {
            for (let i = 0; i < stepped_array.length; i += 1) {
                const idx = stepped_array[i];
                cnt_array[idx] += 1;
                value_array[idx] += (reward * (gamma ** (stepped_array.length - i)) - value_array[idx]) / cnt_array[idx];
                value_array[idx] = Math.floor(value_array[idx] * 10) / 10;
            }

            stepped_array = [];
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
    else {
        if (button2.disabled) {
            button2.disabled = false;
            button.disabled = true;
            env.episodes = 0;
        }
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

\(\gamma = 0.9\)를 사용해서 reward 를 업데이트하면 위의 실행보다는 값의 변화가 뚜렷합니다. 하지만 실행시켰을 때 여전히 목표가 아닌 곳에서 헤매는 비율이 높습니다.

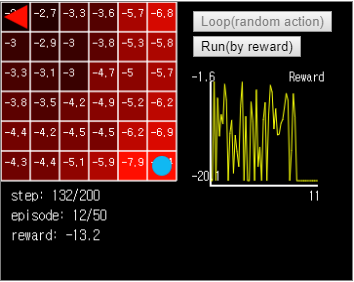그림 13. 이 상태에서 실행시켜보면 에이전트는 (x=0, y=0) 과 (x=1, y=0) 사이를 끝없이 맴돕니다.

이런 불확실성을 없애려면 어떻게 해야 할까요? 오늘 연재글의 제목인 ‘가치 함수’를 계산하면 불확실성을 없애고 에이전트를 아주 빠르게 목표로 보낼 수 있습니다.

가치 함수

각 상태에 대한 가치 함수(value function)을 구해서 가장 가치가 높은 상태로 움직이는 방식으로 이 문제를 풀 수 있습니다. 가치 함수란 말 그대로 상태의 가치를 숫자로 표현한 것입니다. 아래 그림에서 Tic-tac-toe 게임 같은 경우 게임판에 아무 것도 놓이지 않은 상태에서는 가운데 칸의 가치가 0.7 로 가장 높다는 것을 알 수 있습니다.

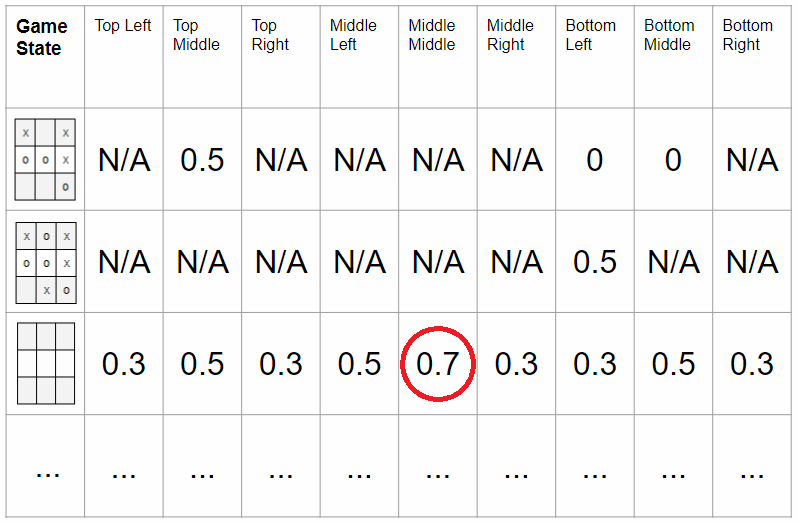그림 14. Tic-tac-toe 게임에서 가운데 칸은 시작 상태일 경우 가장 가치가 높습니다. 이미지 출처 링크

\(\gamma\) 를 사용해서 가치 함수를 계산해보도록 하겠습니다. \(\gamma=0.9\) 를 사용하겠습니다.

모든 상태에 대해서 가치 함수를 처음에는 0 으로 넣습니다. 다만 목표 격자는 도달하면 Episode 가 종료되는 상태이기 때문에 가치 함수를 보상과 같은 값으로 고정시켜서 넣습니다. 즉 목표 격자의 가치는 +1 이 됩니다.

let canvas = document.getElementById('editor_canvas_3');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Get Value';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Get Value x10';
canvas.parentNode.appendChild(button2);

let button3 = document.createElement('button');
button3.style.position = 'absolute';
button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
button3.width = 350 - env.grid_W * env.grid_width - 30;
button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 20).toString() + 'px';
button3.innerHTML = 'Loop(Value)';
canvas.parentNode.appendChild(button3);

let value_array = new Array(env.grid_W * env.grid_W).fill(0);
value_array[value_array.length - 1] = 1;
const gamma = 0.9;

drawValue();
env.draw();

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor(Math.abs(value_array[i]) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function value_iterate() {
    let new_value_array = value_array.slice();
    let x, y;
    let nx, ny;
    let add_value;
    for (let i = 0; i < value_array.length - 1; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        add_value = -Number.MAX_VALUE;
        for (let j = 0; j < dirs.length; j += 1) {
            nx = x + dirs[j][0];
            ny = y + dirs[j][1];
            if (nx >= 0 && nx < env.width &&
                ny >= 0 && ny < env.height) {
                add_value = Math.max(add_value, value_array[nx + ny * env.grid_W] * gamma);
            }
        }

        new_value_array[i] = -0.1 + add_value;
        new_value_array[i] = Math.floor(new_value_array[i] * 100) / 100;
    }
    value_array = new_value_array;
}

button.onclick = function() {
    value_iterate();
    drawValue();
}

button2.onclick = function() {
    for (let i = 0; i < 10; i += 1) {
        value_iterate();
    }
    drawValue();
}

let is_running = false;
let rewards_array = [];

button3.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let values = [];
    let x, y, idx;
    for (let i = 0; i < dirs.length; i += 1) {
        x = agent.x + dirs[i][0];
        y = agent.y + dirs[i][1];
        if (x >= 0 && x < env.width &&
            y >= 0 && y < env.height) {
            idx = x + y * env.grid_W;
            values.push(value_array[idx]);
        }
        else {
            values.push(-Number.MAX_VALUE);
        }
    }

    // find max values
    const m = Math.max(...values);
    values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
    let action = values[Math.floor(Math.random() * values.length)];
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 80);
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';

    button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
    button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 50).toString() + 'px';
});

이때 어떤 격자의 가치는 다음과 같은 수식으로 계산할 수 있습니다.

\[V_{격자} = -0.1 + max(\gamma \times V_{이웃 격자})\]

목표 격자가 아니라면 어디로 움직이든 -0.1 의 보상을 받기 때문에 -0.1 을 더해줍니다. 그리고 이웃 격자 중 가장 큰 가치 함수를 가진 격자로 움직인다고 가정하고 이웃 격자의 가치 함수 중 max 값을 구해서 더해줍니다.

오른쪽의 Get Value 버튼을 누르면 가치를 한번 계산해서 값을 업데이트합니다. 목표 주변의 2개 격자 (x=5, y=4), (x=4, y=5) 들에서 가치가 새로 계산된 것을 확인할 수 있습니다. Get Value 를 여러 번 누르면 시작지점까지 연쇄적으로 가치가 업데이트되지만, 값이 고정된 뒤에는 더 이상 변화가 없습니다.

Loop(Value) 버튼을 누르면 에이전트는 현재 위치한 격자의 이웃 격자의 가치값을 비교해서 높은 값을 가진 격자로 움직입니다. 만약 모든 격자의 값이 같다면 랜덤한 위치로 이동합니다. Grid World 전체의 가치 함수가 계산된 상태라면 에이전트는 즉시 최적의 경로를 찾아냅니다.

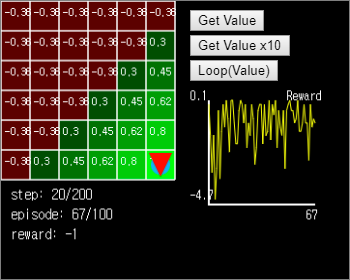그림 15. 가치가 계산된 초록색 영역에서 에이전트는 즉시 최적 경로를 찾아냅니다.

에이전트가 빠지면 페널티를 받는 구덩이를 추가해보면 어떨까요?

let canvas = document.getElementById('editor_canvas_4');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1, 'box': 3}, [[5, 5], [3, 3], [2, 4], [1, 5]]);

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Get Value';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Get Value x10';
canvas.parentNode.appendChild(button2);

let button3 = document.createElement('button');
button3.style.position = 'absolute';
button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
button3.width = 350 - env.grid_W * env.grid_width - 30;
button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 20).toString() + 'px';
button3.innerHTML = 'Loop(Value)';
canvas.parentNode.appendChild(button3);

let value_array = new Array(env.grid_W * env.grid_W).fill(0);
let initial_value_obj = {};
for (let y = 0; y < env.height; y++) {
    for (let x = 0; x < env.width; x++) {
        if (env.grid[y][x].length !== 0) {
            value_array[x + y * env.grid_W] = env.grid[y][x][0].reward;
            initial_value_obj[(x + y * env.grid_W).toString()] = env.grid[y][x][0].reward;
        }
    }
}
const gamma = 0.9;

drawValue();
env.draw();

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor(Math.abs(value_array[i]) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function value_iterate() {
    let new_value_array = value_array.slice();
    let x, y;
    let nx, ny;
    let add_value;
    for (let i = 0; i < value_array.length; i += 1) {
        if (initial_value_obj.hasOwnProperty(i.toString())) {
            new_value_array[i] = initial_value_obj[i.toString()];
            continue;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        add_value = -Number.MAX_VALUE;
        for (let j = 0; j < dirs.length; j += 1) {
            nx = x + dirs[j][0];
            ny = y + dirs[j][1];
            if (nx >= 0 && nx < env.width &&
                ny >= 0 && ny < env.height) {
                add_value = Math.max(add_value, value_array[nx + ny * env.grid_W] * gamma);
            }
        }

        new_value_array[i] = -0.1 + add_value;
        new_value_array[i] = Math.floor(new_value_array[i] * 100) / 100;
    }
    value_array = new_value_array;
}

button.onclick = function() {
    value_iterate();
    drawValue();
}

button2.onclick = function() {
    for (let i = 0; i < 10; i += 1) {
        value_iterate();
    }
    drawValue();
}

let is_running = false;
let rewards_array = [];

button3.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let values = [];
    let x, y, idx;
    for (let i = 0; i < dirs.length; i += 1) {
        x = agent.x + dirs[i][0];
        y = agent.y + dirs[i][1];
        if (x >= 0 && x < env.width &&
            y >= 0 && y < env.height) {
            idx = x + y * env.grid_W;
            values.push(value_array[idx]);
        }
        else {
            values.push(-Number.MAX_VALUE);
        }
    }

    // find max values
    const m = Math.max(...values);
    values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
    let action = values[Math.floor(Math.random() * values.length)];
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 80);
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';

    button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
    button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 50).toString() + 'px';
});

노란색 네모를 (x=1, y=5), (x=2, y=4), (x=3, y=3) 세 곳에 배치했습니다. 이곳에 도달하면 에이전트는 -1 의 보상을 받습니다.

Get Value 버튼을 눌러서 각 상태의 가치함수를 업데이트하면, 위에서 정했던 규약대로 노란색 네모가 있는 곳은 -1 로 업데이트되지 않는 것을 확인할 수 있습니다. 여러 번 눌러서 가치함수를 업데이트하면 Grid World 의 왼쪽 아래는 가치함수의 도달이 느린 것을 알 수 있습니다. Loop(Value) 버튼을 눌러서 에이전트를 움직여보면 막힌 구간을 피해서 오른쪽 위 경로로 이동해서 목표에 도달하는 것을 확인할 수 있습니다.

이것으로 강화학습의 기본 환경 중 하나인 Grid World 와 기본적인 알고리즘 중 하나인 가치함수의 계산법과 활용에 대해 알아보았습니다. 다음 시간에는 좀 더 어려운 문제를 제시하고, 그것을 풀기 위한 더 효율적인 알고리즘을 제시하는 글로 찾아뵙겠습니다. 긴 글 읽어주셔서 감사합니다.

Grid World 의 스타일은 Maxime Chevalier-Boisvert 의 gym-minigrid 를 참고했습니다. ↩

greentec's blog game designer, scripter, researcher

강화학습 알아보기(1) - 가치 함수

강화학습이란?

이론적 배경

Grid World

가치 함수

Related Posts

Linkedin의 Queens 게임 맵 만들기 13 May 2024

Shadertoy 'Bleepy blocks' 분석 03 May 2021

『시작하세요! 텐서플로 2.0 프로그래밍』 재고 추적 자동화 01 Mar 2020