Shadertoy 불 쉐이더 분석

15 Dec 2018 • 0 Comments

• 도입
• random
• noise
• fbm
• bumpMap
• 기타 효과들

“Pyroclastic fireball” by Duke

 

도입

오늘은 shader 에서 가장 기본이 되는 것들 중 하나인 fire shader 를 살펴보려고 합니다. 여기서 random, noise, fbm, bumpMap 등 shader 의 기초적인 구성요소들을 하나씩 짚어보면서 Shadertoy 에 사용된 fragment shader 에서 이것들을 어떻게 표현할 수 있는지를 알아볼 것입니다.

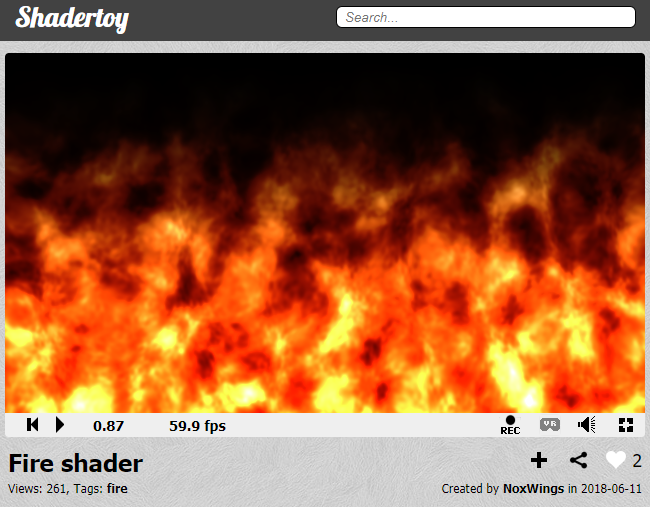
이번에 분석할 Shadertoy 의 코드는 많은 fire 관련 shader 중에서 단순한 편에 속하면서도 필요한 내용을 빼곡하게 담고 있는 Fire Shader입니다. 이 코드를 처음 봤을 때 마치 누군가 저를 위해 예제코드를 써준 것 같아서 너무 행복했습니다. 그럼 시작해보겠습니다.

 

random

대부분의 프로그래밍 언어에서 랜덤 함수는 간단한 형태로 불러와서 즉시 사용할 수 있습니다. javascript 에서는 Math.random() 이 0.0 이상 1.0 미만의 값을 반환합니다. python 에서는 import random 으로 random 라이브러리를 불러온 다음에 random.random() 으로 같은 일을 할 수 있습니다.

shader 에는 이렇게 간편하게 쓸 수 있는 함수가 없습니다. 대신 2가지 선택지가 있는데요. 하나는 랜덤한 값(주로 흑과 백의 noise)이 칠해져 있는 image 를 불러오는 것과, 직접 랜덤함수를 만들어서 쓰는 것입니다.

Shadertoy 에서 기본적으로 제공하는 noise 이미지들. 코드 하단의 iChannel0~4 를 누르고 Texture 를 선택하면 나옵니다. 이에 대한 설명은 다른 글에서 다루겠습니다.

오늘은 직접 랜덤함수를 만들어서 쓰는 방법을 알아보겠습니다. The book of shaders 의 이 글과 이 코드와 동영상 등에 이미 좋은 설명들이 자세하게 나와 있습니다만, 그래도 좀 더 자세히, 가급적이면 쉽게 설명해보려고 합니다.

랜덤한 수, 한자어로 난수란 주기성을 갖지 않는, 예측할 수 없는 수 를 말합니다. 여기서 주기성이란 같은 수가 반복되는 성질입니다. 다음의 수열을 한번 살펴보겠습니다.

1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, 5, 4, 3, 2, 1, 2, 3, 4, ...

여기서 1은 1번째, 9번째, 16번째에 나오고 있습니다. 이 수열이 계속 이어진다고 했을 때 다음에는 16에 7을 더한 23번째에 1이 나올 것이라고 예측할 수 있습니다. 그리고 1~5 까지의 숫자들은 반복되며 계속 등장하고 있습니다. 즉 이 수열은 주기성도 갖고 예측할 수도 있기 때문에 랜덤이 아닙니다. 이런 수로 암호를 만들면 상대방에게 즉시 간파당할 것이고, 유니크 아이템 드랍 테이블을 만들면 대부분의 유저가 유니크 아이템을 얻어서 게임 내 밸런스는 붕괴될 것입니다.

그럼 이런 수열은 어떨까요?

1, ?, ?, ?, ?, ?, ?, ?, 1, ?, ?, ?, ?, ?, ?, ?, 1, ?, ?, ?, ...

여기서 ? 로 표시한 수는 예측이 불가능한 수입니다. 이런 수를 만들어낼 수 있다면 좋겠지만, 여전히 1번째, 9번째, 16번째, … 에 오는 1 은 예측 가능합니다. 그렇다면 1이 나오는 주기가 늘어난다면 어떨까요?

1, ?, ?, ...(매우 많은 수의 ?), ?, ?, 1, ?, ?, ..., ?, ?, 1, ?, ?, ...

아직 주기성은 가지고 있지만, 나머지 숫자는 거의 ? 이기 때문에 예측이 거의 불가능한 수열이 될 것입니다. 이것이 바로 컴퓨터에서 보편적으로 사용하는 난수 생성기(Random Number Generator)입니다. 컴퓨터는 수식으로 난수를 만들기 때문에 주기성을 갖는 것은 어쩔 수 없지만, 그 주기를 최대한 늘려서 예측이 거의 불가능한 난수를 만들어냅니다.

PHP 의 내장함수가 만든 랜덤(왼쪽)과 Random.org 에서 생성한 랜덤의 비교. 왼쪽에서 패턴(주기성)이 보이는 것을 확인할 수 있습니다. 오른쪽이 만든 랜덤의 품질이 상대적으로 더 좋다는 것을 알 수 있습니다. 출처 링크

그럼 이제 shader 에서 어떻게 랜덤 함수(난수 생성기)를 만드는지에 대해서 코드와 함께 알아보겠습니다.

uniform float a; uniform float b; uniform float c; float rand(vec2 co) { return fract(sin(dot(co.xy, vec2(a, b))) * c); } void main() { float x = rand(gl_FragCoord.xy); gl_FragColor = vec4(x, x, x, 1.0); }

이 함수, float rand(vec2 co) 의 기원은 아직 정확하게 밝혀진 바가 없습니다. 이와 관련된 논의가 stack overflow 에 올라온 적이 있습니다만, 여기서도 정확한 기원을 밝히는 데에는 실패했습니다. 기원은 몰라도 지금은 shader 쪽에서 가장 유명하고 널리 쓰이는 함수중의 하나가 되어버렸습니다.

위의 range slider 를 변화시키면서 a, b, c 에 각기 다른 값을 세팅해보면, 그럴듯한 랜덤값이 나올 때도 있지만 아래 이미지처럼 규칙적인 값이 나올 때도 있습니다. 애초에 이 함수를 만든 사람이 a=12.9898, b=78.233, c=43758.5453 를 어떤 기준으로 정했는지도 알 수 없지만, 거의 대부분이 이 값을 고치지 않고 그대로 쓰고 있습니다. 우리도 이 값을 그대로 써도 될 것 같습니다.

a=3.244, b=19.464, c=44569.8166 일 때 입니다. 이 밖에도 a,b,c 를 각각 0으로 세팅하거나 다른 값으로 세팅할 때 가끔 품질이 나쁜 랜덤이 생성되는 것을 확인할 수 있습니다.

이 함수는 2D 이미지의 각 픽셀에 대해서 간단하게 0.0~1.0 사이의 랜덤값을 만들어줍니다. 8행에서 uv 를 사용하는 대신 gl_FragCoord 만 사용해서 랜덤값을 계산한 것을 확인할 수 있습니다. float rand(vec2 co) 함수는 co 자리에 변수를 넣으면 랜덤값을 계산해줍니다. 물론 이 랜덤값은 수식으로 계산되었기 때문에 예측가능하지만 주기가 긴 유사랜덤값이라는 것을 앞에서도 말씀드렸습니다.

dot 는 dot product, 내적이라는 의미로 각 구성요소들을 서로 곱한 후 더해준다는 의미입니다. 예를 들어서 gl_FragCoord.xy 와 vec2(a,b) 를 dot 연산한다면, gl_FragCoord.x * a + gl_FragCoord.y * b 와 같은 값이 됩니다. dot 연산의 결과값은 언제나 float 이 됩니다.

sin 은 우리가 이 시리즈에서 계속 만나고 있는 삼각함수의 sin 입니다. Shadertoy 메타볼 분석에서는 각 메타볼의 중심 좌표를 변하게 하기 위해서 sin 이 쓰였습니다. 여기서도 sin 은 입력값을 변화시키고, 주기성을 갖게 합니다.

주기성을 갖는다는 것은 랜덤에 좋지 않은 요소이지만, 그 주기가 매우 크면 예측이 힘들어진다고 위에서 말씀드렸습니다. 이쪽을 담당하는 것이 바로 sin 에 곱해지는 c 입니다. 43758.5453 은 매우 큰 값이기 때문에 sin 함수의 주기도 커집니다.

fract 는 이 함수에서 가장 핵심적인 부분입니다. fract 는 fraction 의 줄임말입니다. 실수는 정수부와 소수부로 나눌 수 있는데, 이 중 소수부를 영어로 fractional part 라고 합니다. fract 는 이 중 정수부를 날리고 소수부만 반환합니다. 지난 글에 나왔던 floor 와는 반대되는 기능을 하는 함수입니다.

The book of shaders 의 random 페이지에서 이쪽에 관련된 설명을 아주 깔끔하게 하고 있습니다. 저도 이쪽을 많이 참고하여 나름대로 재현해 보았습니다.

처음에는 평범한 y = sin(x); 의 그래프를 보실 수 있습니다. 2행의 주석을 해제하면 y = sin(x) * 5.0; 이 됩니다. 함수의 기울기가 커지면서 변화폭이 커지는 것을 알 수 있습니다. 이 말은 아주 약간만 x 값이 변해도 y 값이 변하는 양이 커진다는 것입니다.

3행의 주석을 해제해보면, sin(x) 값이 0.0~1.0 사이로 제한되는 것을 확인할 수 있습니다. 소수부만 남겼기 때문입니다. 4행의 주석을 해제하면 변화가 좀 더 불규칙해진 것을 확인할 수 있습니다. 계속해서 5행, 6행의 주석을 해제해보면, 오른쪽으로 한 스텝 이동할 때 다음 값이 무엇이 될지 도저히 예측할 수 없을 정도라는 것을 알게 됩니다. 이렇게 큰 수를 곱한 sin 함수의 소수부 fract 를 취해서 랜덤한 값을 얻을 수 있습니다.

 

noise

random 과 noise 는 무엇이 다른 걸까요? 간단히 말해서 shader 에서 사용하는 noise 에는 주변에 대한 연속성 이 있습니다. 즉 (x,y) 와 (x+1,y) 사이에 부드럽게 변하는 값을 가지게 됩니다.

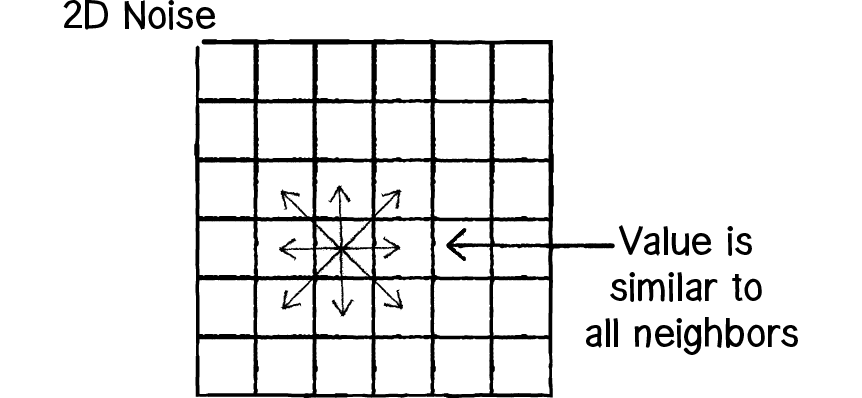noise 의 값은 주변에 대해서 연속성을 가집니다. 출처 링크

반면에 위에서 봤던 random texture 는 주변에 상관없이 독립적인 값을 가집니다. 위에서 살펴본 것처럼 예측 가능하지 않아야 하기 때문 입니다. 결국 random 으로 noise 를 만드는 작업은 예측 가능하지 않은 rand 함수로 연속성을 가진 예측 가능한 noise 를 만드는 작업입니다.

float rand(vec2 co) { return fract(sin(dot(co.xy ,vec2(12.9898,78.233))) * 43758.5453); } vec2 hash( vec2 p ) { p = vec2( dot(p,vec2(127.1,311.7)), dot(p,vec2(269.5,183.3)) ); return -1.0 + 2.0*fract(sin(p) * 43758.5453123); }

그런데 사실 여기서 분석 중인 fire shader 에서는 rand 함수는 정의만 해놓고 사용하지 않았습니다. 대신 사용한 것이 바로 4행에 나오는 hash 함수입니다. rand 함수는 1개의 output 을 내기 때문에 반환형이 float 이지만, hash 함수는 비슷한 구조에서 2개의 output 을 내기 때문에 반환형이 vec2 인 것을 눈여겨 봐주시기 바랍니다. 그리고 0.0~1.0 사이의 output 이 나오는 rand 에 비해 hash 는 -1.0~1.0 사이의 output 을 냅니다. 그 이유는 hash 의 결과를 바로 gl_FragColor 에 쓰려는 것이 아니고, 다른 함수인 noise 에서 불러와서 쓰려고 하기 때문입니다.

hash 함수의 output 을 0.0~1.0 으로 바꿔서 그 중 첫번째인 x 값만 color 로 쓰면 rand 와 동일합니다. 12행의 주석을 해제해서 랜덤 값을 y 로 바꿔보면 이미지에 패턴이 조금 보이는데, y 를 계산하는 데 쓰인 숫자들이 썩 좋은 숫자가 아닌 것을 알 수 있습니다. 하지만 나중에 계산할 fire shader 의 결과에 큰 영향은 미치지 않습니다.

아래의 내용은 sin 을 사용하지 않는 hash 에 대한 내용입니다. 나중에 다른 글에서 관련된 내용을 소개할 예정이니, 이 글의 내용만 보고 싶으신 분은 일단 넘어가셔도 괜찮을 것 같습니다.

Hash without Sine 이라는 Shadertoy 코드를 보면, 계속 켜놓았을 때 2초 후부터 왼쪽과 오른쪽에 차이가 생기기 시작하고, 점점 그 차이는 커집니다. 랜덤한 수를 계속 생산할 때 왼쪽의 hash 함수를 사용한 결과가 오른쪽의 sin 함수에 비해서 훨씬 안정적인 것을 확인할 수 있습니다. sin 은 정밀한 계산을 위해 제작된 함수가 아니고, GPU 마다 계산 결과에 차이가 있기 때문이라고 합니다.

hash 는 원래 암호화에 사용되는 함수의 이름입니다. 어떤 값을 input 으로 넣든 일정한 규칙에 따라 output 을 반환하게 됩니다. 이때 나오는 output 은 랜덤하고 거의 예측이 불가능한 성질을 갖습니다. sin 에서 주기가 돌아오면 같은 output 이 나오는 것처럼, hash 에는 함수의 규칙에 따라 어떤 2개의 입력이 동일한 output 을 낼 확률이 있습니다. 이를 hash 충돌 이라고 합니다.

하지만 이 hash 충돌이 일어날 가능성이 낮다면 shader 에서는 충분히 랜덤 함수로 사용할 수 있습니다.

2017년 9월에 Inigo Quilez 는 sin 을 사용하지 않는 빠른 hash 함수를 여러 개 소개했습니다. 이 함수들에 대해서는 다른 글에서 소개할 수 있도록 하겠습니다.

fire shader 에서 쓰인 hash 는 이와는 달리 sin 을 사용합니다. 오해의 소지가 있기 때문에 사실 함수 이름을 rand2 로 바꿔도 괜찮을 것 같습니다.

그럼 여기서 쓰인 noise 는 어떤 함수일까요? 매우 복잡한 코드였는데, 기원을 찾아보니 역시 Inigo Quilez 가 가장 처음 Noise - simplex - 2D 에서 작성한 코드였습니다. 그리고 이 함수는 Simplex noise 를 계산하고 있다는 것도 알게 되었습니다.

최초의 noise 는 Ken Perlin 이 1983년에 만들었는데 그래서 Perlin noise 라고 불립니다. 2001 년에 Ken Perlin 은 자신이 만들었던 Perlin noise 에서 가끔 방향성이 뚜렷하게 보이는 결점과 계산속도를 개선한 버전을 내놓았는데 이것이 바로 Simplex noise 입니다.

사실 두 noise 의 결과물은 눈으로 보기에는 큰 차이를 보이지 않습니다. 아래 코드에서 왼쪽이 Simplex noise(noise), 오른쪽이 Perlin noise(noise_p) 입니다. Perlin noise 가 구름 같은 모양이 아니네? 라고 생각하시는 분도 계실텐데요, 여기에 같은 noise 를 frequency 를 바꿔가면서 여러 개 더하면 포토샵에서 쉽게 만들 수 있는 구름 이미지 같은 Fractal noise 가 됩니다. 아래에서 설명드릴 fbm 이 바로 Fractal Brownian Motion 의 약자로 이런 Fractal noise 를 생성하는 함수입니다.

47 행과 50 행에서 noise 안의 uv 에 각각 10., 16. 을 곱해주는 것을 보셨나요? 이 숫자를 1. 로 바꾸면 어떻게 될까요? 또 100. 처럼 큰 숫자로 바꾸면 어떻게 될까요?

작은 숫자로 바꿨을 때는 이미지가 희미해지고 패턴이 단순해집니다. 반대로 큰 숫자로 바꾸면 random texture 와 비슷하게 패턴을 찾기 힘든 이미지에 가까워집니다. 여기서 작은 숫자, 큰 숫자는 카메라의 zoom in, zoom out 이라고 생각해볼 수 있습니다. 작은 숫자를 곱하면 noise texture 의 작은 부분이 확대되어서 나타나고, 큰 숫자를 곱하면 넓은 부분을 표시할 수 있게 됩니다. 여기서 곱하는 숫자를 frequency 라고 합니다. frequency 란 진동수, 즉 주기적인 현상이 단위시간 동안 몇 번이 일어났는지를 정의하는 말입니다. frequency 가 작으면 변화도 작고, frequency 가 크면 변화량도 큽니다.

noise 의 가장 중요한 역할은 보간(interpolation) 입니다. 즉 서로 인접해 있는 noise 값 사이를 부드럽게 연결해주는 것입니다. Perlin noise 는 사각형의 grid 에서 인접한 4개의 꼭지점 사이에 있는 값을 interpolation 해주는 방법이고, Simplex noise 는 삼각형의 3개의 꼭지점 사이에 있는 값을 interpolation 해주는 방법이라고 말할 수 있습니다. ¹

frequency 가 작으면 좁은 영역을 확대해서 보여주기 때문에 보간되는 영역이 잘 보이고, frequency 가 커질수록 보간되는 영역이 거의 보이지 않게 됩니다.

noise texture 는 보간된 이미지이기 때문에 기본적으로 흐릿합니다. 이 이미지의 디테일을 뚜렷하게 살려주고 우리가 많이 봤던 포토샵 구름 같은 이미지를 만들어주는 함수가 바로 fbm 입니다.

 

fbm

noise 이미지는 흐릿해서 실사용에 무리가 있습니다. 이를 보완하는 것이 Fractal noise 입니다.

왼쪽이 noise, 오른쪽이 fbm 함수의 결과물입니다. fbm 쪽에서 훨씬 디테일한 표현이 되고 있는 것을 알 수 있습니다.

코드는 간단한 편이니 분석해보도록 하겠습니다. 28행의 mat2 는 2개의 row 와 2개의 column 을 가지는 float matrix 입니다. 여기서는 회전변환과 확대변환이 곱해진 모습입니다. 즉 이렇게 다시 쓸 수 있습니다.

\[\left[\begin{matrix}1.6 & 1.2 \\ -1.2 & 1.6\end{matrix}\right] = \left[\begin{matrix}0.8 & 0.6 \\ -0.6 & 0.8\end{matrix}\right] \times \left[\begin{matrix}2 & 0 \\ 0 & 2\end{matrix}\right]\]

앞의 행렬은 회전변환, 뒤의 행렬은 확대변환입니다. 확대는 단위행렬인 \(\left[\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}\right]\) 에 2를 곱했기 때문에 2배로 키워준 모습이고, 회전은 \(\left[\begin{matrix}cos(\theta) & sin(\theta) \\ -sin(\theta) & cos(\theta)\end{matrix}\right]\) 에서 \(cos(\theta)=0.8, sin(\theta)=0.6\) 이 되는 약 36.8도로 회전시켜주는 것을 알 수 있습니다.

29-32 행에서는 f 에 noise(p) 를 더해주는데, 계수를 각각 0.5000, 0.2500, 0.1250, 0.0625 로 1/2 로 감소시켜가며 더해주고 있습니다. 이렇게 되면 나중에 더해지는 값은 영향력이 점점 줄어드는 값이 됩니다.

그리고 p=m*p; 로 방금 본 변환행렬을 곱해줍니다. 회전변환은 같은 p 를 곱하기 때문에 회전을 시켜서 방향성(패턴)을 보이지 않도록 하는 것이고, 확대변환은 앞에서 본 frequency 를 키워주는 것과 같은 효과입니다. frequency 가 커지면 패턴을 찾기 힘든 세밀한 이미지가 되었던 것을 기억하시나요? 세밀한 이미지일수록 계수를 감소시키기 때문에 fbm 함수의 최종 결과물에 끼치는 영향은 줄어들지만, 그래도 영향이 미미하게 존재합니다. 그 디테일이 왼쪽과 오른쪽의 차이를 만들어냅니다.

마지막 33행에서는 -1.0~1.0 사이인 결과값을 0.0~1.0 사이로 보정해서 출력합니다. 바로 color 값으로 쓸 수 있는 출력 범위입니다.

fbm 에 대해서는 fbm 에 다시 fbm 을 씌우는 식으로 더 멋진 결과물을 만들어내는 Inigo Quilez 가 쓴 응용편이 있어서 읽어보셔도 좋을 것 같습니다. 이 부분도 중요해서 나중에 다뤄야할 것 같습니다.

 

bumpMap

저는 사실 이 글을 며칠째 쓰고 있습니다. 지금 bumpMap 을 쓰는 시점이 글을 시작한지 4일 정도 지난 시점이네요. 글쓰는 스타일이 앞에서 막히면 자료를 찾고 다음으로 넘어갈 때까지 못 쓰는 스타일이라 좀 오래걸린 것 같습니다. 그래도 앞에서 중요한 내용들을 많이 다뤘기 때문에, 상대적으로 후반부는 빠르게 넘어갈 수 있을 것 같습니다.

bump 라는 단어에는 충돌, 혹 등의 뜻이 있습니다. bump 라는 단어가 우리 생활에서 친숙한 경우 중 하나는 자동차의 범퍼(bumper)가 되겠습니다. 범퍼는 자동차의 앞뒤에서 오는 충격을 흡수하는 소모 부품입니다.

bumpMap 함수는 표면의 디테일을 normal 이라는 형태로 추가해줍니다. ² normal 이란 물체의 중심에서 바깥쪽으로 향하는 표면의 방향 벡터입니다. 법선벡터라고도 합니다. 사실 지금은 3D 가 아닌 2D 영역만 다루고 있기 때문에 여기서의 표면은 실제로 돌출된 부분은 아닙니다.

좌측은 fbm, 우측은 bumpMap 의 계산 결과인 normal 입니다. 이미지가 전반적으로 푸르스름한데, normal 벡터의 x, y, z 를 각각 R, G, B 채널에 저장하기 때문입니다. x, y 는 각각 0.0~1.0 사이의 값을 가지는 반면에, 44행에서 z 에는 1. 값을 줬습니다. 따라서 이미지가 파란색으로 보이는 것입니다.

나머지 코드도 살펴보면, 38행에서는 1./resoultion.xy 를 해준 값을 s 에 저장하고, 40-41 행에서 그 값에 vec2(1.,0), vec2(0,1.) 을 곱하는 것을 볼 수 있습니다. 스크린 기준으로 uv 지점에서 x 축으로 1픽셀, y 축으로 1픽셀 떨어진 점에 대해서 fbm 을 구하는 식임을 알 수 있습니다.

43 행에서는 x 축의 차이, y 축의 차이를 구한 다음에 미리 정의된 normalStrength 를 곱해서 normal 을 강하게 확보합니다. 1 행에 정의된 이 값을 바꿔보면 오른쪽 이미지가 흐릿하게 또는 강렬하게 바뀌는 것을 확인할 수 있습니다. xy 는 -normalStrength 부터 normalStrength 까지 나올 수 있겠지만, fbm 의 값은 연속된 구간에서 조금씩 변하기 때문에 실제 값은 매우 작을 것입니다. 그렇기 때문에 큰 normalStrength 를 곱해주는 것입니다.

44 행에서는 xy 에 .5 를 더해줍니다. .5 가 중앙값이기 때문입니다. 이보다 작으면 음의 방향, 크면 양의 방향을 나타내게 됩니다.

 

기타 효과들

그럼 위에서 계산한 normal 이 실제로 어떻게 fire shader 를 만드는 데에 쓰이는지 알아보겠습니다.

bumpMap 으로 계산된 normal 이 time 의 영향을 받아서 위쪽으로 이동하고 있습니다. 5 행의 distortionMovement 에 y 값이 -0.3 으로 들어가 있기 때문에 위쪽으로 이동하는 것입니다. 이 값을 바꿔볼 수 있고, x 값도 바꿔볼 수 있습니다.

52 행에서 uv 에 곱해지는 vec2(1.0, 0.3) 도 눈여겨 봐주시기 바랍니다. 1.0 을 곱하면 값에 변화가 없겠지만, 0.3 을 곱하면 frequency 가 작아지는 효과를 갖게 됩니다. 따라서 위아래로 길쭉한 이미지가 만들어지게 되는 것입니다.

그 다음으로는 displacement 가 쓰였습니다. 이 기법은 3D 에서 bumpMap 이나 normalMap 과 다르게 실제로 3D geometry 의 모양을 변화시킵니다. 2D 에서는 포토샵에서 볼 수 있는 것 같은 물결 이펙트 등을 내는 데에 사용됩니다.

출처 링크

여기서 쓰인 displacement 를 gl_FragColor 로 뽑아보면 어떤 일이 일어나는지를 명확하게 알 수 있습니다.

왼쪽은 normal, 오른쪽은 displacement 입니다. color 값 표시를 위해서 -1.0~1.0 사이로 제한된 값을 0.0~1.0 으로 바꿨습니다. 흐릿하지만 뭔가 움직이고 있는 모습이 보입니다. distortionStrength 를 10.1 같은 큰 값으로 줘보면 확실히 뭔가 변하고 있다는 것을 알 수 있습니다.

57 행을 자세히 들여다보면 bumpMap 의 계산 결과로 xy 에 더해주었던 0.5 를 다시 뺀 것을 알 수 있습니다. 그리고 distortionStrength 를 곱해준 다음에, 최소값과 최대값 사이로 출력값을 제한해주는 clamp 는 내장 함수를 이용해서 출력값을 -1.0~1.0 사이로 제한했습니다.

여기까지 오면 사실 앞에서 설명드린 bumpMap 이나 normal 은 모두 이 displacement 를 구하기 위한 과정이었다는 것을 알 수 있습니다. 코드의 다른 곳에서는 bumpMap 과 normal 이 쓰이는 곳이 없습니다.

displacement 가 제대로 작동하는지 확인하기 위해서는 코드를 좀 더 봐야합니다. displacement 는 그 자체로서 의미를 가지기보다는 불 텍스쳐에 영향을 끼치는 역할을 하기 때문입니다.

드디어 불 텍스쳐에 가까운 이미지가 모습을 드러냈습니다. 54 행에서는 displacement 를 uv 에 더해주고, 56 행에서는 uvT 를 계산합니다. uv Texture 의 준말인 듯 합니다. 52 행과 구조가 비슷한 점을 주목해주십시오. y 에 곱하는 값이 0.5 로 위아래가 길쭉한 이미지를 만들고, fireMovement 도 y 의 속도가 -0.5 로 위쪽으로 올라가는 모습입니다.

fireMovement 의 y 를 0.5 로 바꿔보면 이미지가 일렁거리는 것을 확인할 수 있는데, 이는 displacement 에 의해 전체 좌표는 위쪽으로 이동하고 있지만 이미지 자체가 아래쪽으로 내려가게 바꿔서 displacement 를 잘 관찰할 수 있게 된 것입니다.

57 행에서는 frequency 에 8.0 을 주면서 fbm 값을 얻고 있습니다. 이 값을 변화시키면 이미지에 어떤 영향이 있는지는 앞에서 많이 말씀드린 것 같습니다. pow 함수는 거듭제곱을 계산하는 내장 함수입니다. 지수가 1.0 이기 때문에 계산은 따로 하고 있지 않지만, 숫자를 바꿔보면 이미지가 진해지거나 연해지는 것을 확인할 수 있습니다. 값이 0.0~1.0 사이의 수이기 때문에 거듭제곱이 1보다 크면 값은 더 작아지고, 반대이면 값은 더 커집니다.

마지막으로 불의 강도에 관여하는 gradient 와 색상을 살펴보겠습니다.

59 행에 앞에서 나온 pow 내장 함수가 다시 나왔습니다. \(5 \times (1 - uv.y)^2\) 는 uv.y 가 0.0~1.0 사이일 때 5.0~0.0 의 값을 가지게 되고, y 가 작을수록 큰 값을 가진다는 것을 알 수 있습니다. 60 행의 finalNoise 는 여기에 n 을 곱해서 n 은 y 가 작을수록 큰 값을 갖게 됩니다.

62 행은 finalNoise 에 color 의 계수가 될 값을 곱해줍니다. n 은 fbm 의 출력이기 때문에 0.0~1.0 사이의 값을 갖습니다. 따라서 거듭제곱할수록 값이 작아지게 됩니다. R 채널과 달리 G, B 채널은 거듭제곱을 해서 붉은색이 강조되도록 한 것을 알 수 있습니다.

이제 63 행의 주석을 해제하고 64 행을 주석처리하면 최종 fire shader 를 확인할 수 있습니다. 여기에 나온 여러 변수들을 바꿔보면서 자신만의 fire shader 를 실험해보시길 바랍니다.

fireMovement.y = 0.5, distortionStrength = 0.8, color = finalNoise * vec3(2. * n * n * n, 2. * n * n * n, n);

이것으로 길었던 fire shader 분석글을 마치려고 합니다. 다음 시간에는 조금 쉽고 짧은 코드로 돌아오려고 합니다. 긴 글 읽어주셔서 감사합니다.