Shadertoy 빗방울 효과 분석

• 도입
• Texture 입력
• 빗방울
• 사라지는 빗방울

“Heartfelt” by BigWIngs

도입

오늘은 Shadertoy 에 많이 보이는 효과 중 하나인 빗방울 효과를 분석해보겠습니다. 분석할 코드는 ‘Rain drops on screen’입니다. 코드에 주석이 꼼꼼하게 달려 있어서 분석하는 데에 많은 도움이 되었습니다. 그럼 시작해보도록 하겠습니다.

‘Rain drops on screen’ by eliemichel

Texture 입력

예전에 Shadertoy 불 쉐이더 분석 에서 Shader 에서는 inline function 으로 사용할 수 있는 랜덤 함수가 없기 때문에, 두 가지 방법으로 랜덤값을 사용할 수 있다고 했습니다. 첫번째는 직접 hash 같은 랜덤 함수를 만들어서 사용하는 것이고, 두번째는 랜덤 텍스처를 불러오는 방법입니다. 오늘은 두번째 방법을 사용해보도록 하겠습니다.

Shadertoy 에서는 다양한 입력 텍스처를 제공합니다. 이들은 iChannel0~iChannel3 이라는 이름으로 불러올 수 있습니다. 여기서는 간결하게 texture0 이라는 이름으로 불러와보겠습니다.

texture2D 에서 첫번째 인수는 표시할 텍스처이고, 두번째 인수는 텍스처의 좌표를 의미합니다. 두번째 인수로 들어간 uv 는 화면 전체의 픽셀들을 0.0~1.0 범위로 고정해주기 때문에, 스크린에는 텍스처가 온전하게 들어갑니다.

6행의 주석을 해제해보면 이미지가 확대됩니다. uv 의 범위가 0.0~1.0 에서 0.0~0.5 가 되기 때문에 왼쪽 아래의 4분면만 표시되는 것입니다. 7행의 주석을 해제해보면 반대로 이미지가 좁은 영역에 표시되는 것을 볼 수 있습니다. 그런데 나머지 영역도 모두 채우는 타일링 기법을 쓰려면 어떻게 해야 할까요? uv 에 반복시키고 싶은 값은 그대로 곱한 다음에 실수에서 정수 부분을 없애는 fract 를 쓰면 쉽게 이 문제를 해결할 수 있습니다. 8행의 주석을 해제하셔서 확인하시기 바랍니다.

texture2D 에는 세번째 인수도 넣을 수 있는데 이것은 bias 로 텍스처의 LOD¹를 계산할 때 mipmap 레벨에 더해지는 값입니다. 0.0 이면 아무런 변화가 없고, 9행의 주석을 해제하면 1.5 가 bias 로 적용되어 이미지가 흐릿해지는 것을 볼 수 있습니다. 원래 코드에서는 LOD 에 직접 접근할 수 있는 textureLod 도 사용하고 있지만, OpenGL ES 2.0 스펙에서 textureLod 는 vertex shader 에서만 사용할 수 있고(관련 링크), 이 코드에서는 배경 이미지를 흐릿하게 만드는 데에만 사용되고 있기 때문에 여기서는 textureLod 를 굳이 사용하지 않겠습니다.

앞에서 말씀드린 것처럼 랜덤 텍스처도 입력으로 받을 수 있습니다.

위 코드는 “Simple Texture Distort” by mikiex 를 참조해서 작성했습니다. texture0 에는 위에서 사용했던 거리 풍경 텍스처를, texture1 에는 랜덤 텍스처를 사용했습니다. texture1 의 랜덤값에서 r 채널과 g 채널을 이용해서 texture0 의 uv 값에 살짝 변화를 줘서 왜곡되는 효과를 만듭니다.

위에서 참조한 코드의 결과보다 본문의 결과가 좀 더 뿌옇게 보입니다. 이는 사용한 랜덤 텍스처의 차이 때문입니다. 참조한 코드는 64x64 랜덤 텍스처를 사용했고, 여기서는 256x256 랜덤 텍스처를 사용했습니다. 참조한 코드와 비슷한 효과를 보고 싶다면 7행의 주석을 해제하면 됩니다. 랜덤 텍스처의 가로, 세로 각각 1/4 크기만 사용하기 때문에 64x64 랜덤 텍스처를 사용한 것과 비슷한 효과를 보입니다.

그럼 다시 원래 코드로 돌아와보도록 하겠습니다. Rain drops on screen 8행은 다음과 같습니다.

n = texture(iChannel1, u * .1).rg;  // Displacement

n 은 7행의 vec2 가 적용되기 때문에 역시 vec2 n 이 됩니다. iChannel1 은 랜덤 텍스처입니다. u 는 uv 입니다. 이것을 화면에 직접 나타내보면 아래와 같습니다.

6행의 주석을 해제해보면 원래 랜덤 텍스처가 오밀조밀한 것을 확인할 수 있습니다. 5행에서는 .1 을 곱해서 랜덤 텍스처의 작은 영역만 사용하면서 보간(interpolation)이 된 것입니다.

이렇게 계산된 n 은 빗방울에서 쓰이게 됩니다. 참고로 원래 코드의 8행에서 .1 을 1.0 으로 바꾸거나 곱하는 부분을 아예 없애보면, 빗방울이 매우 작아지는 것을 확인할 수 있습니다. 그리고 반대로 더 작은 .001 같은 값을 곱해보면 빗방울이 완벽한 원에 가까워지게 됩니다. 왜 이렇게 되는지는 다음 섹션에서 설명해드리도록 하겠습니다.

빗방울

빗방울은 for-loop 안에서 계산되고 있습니다. for-loop 를 주석처리하면 빗방울은 사라지고 흐릿한 배경만 남습니다. 그럼 for-loop 의 첫 줄부터 하나씩 분석해보겠습니다.

vec2 x = iResolution.xy * r * .015,  // Number of potential drops (in a grid)
     p = 6.28 * u * x + (n - .5) * 2.,
     s = sin(p);

첫 부분의 x 를 구성하는 요소들은 r 외에는 고정된 값만 존재합니다. iResolution 은 제 컴퓨터 모니터의 shadertoy 창에서 640x360 이니까 여기에 r 과 .015 를 곱하면 r=1, iResolution.x=9.6, iResolution.y=5.4 가 나오게 됩니다.

p 는 두 항의 합입니다. 첫번째 항인 6.28 * u * x 에서 6.28 은 \(2 \pi\) 의 근사값입니다. u 는 uv 이고, x 는 앞에서 구해준 값입니다. 대충 계산해보면 r=1 일 때 첫번째 항의 범위는 (0.0,0.0)~(60.288,33.912) 가 될 것입니다. 숫자상으로는 아직 특별한 것이 보이지 않습니다.

두번째 항인 (n - .5) * 2. 는 n 의 범위가 랜덤 텍스처의 color 값이기 때문에 0.0~1.0 이고, 여기에서 -.5 를 해주면 -0.5~0.5, * 2. 를 해주면 -1.0~1.0 이 됩니다. 첫번째 항보다는 작은 값이긴 합니다만, 매 픽셀마다 이 값이 더해지기 때문에 규칙적이지 않은 값이 만들어집니다.

세번째 줄에서는 p 에 sin 함수를 취해서 -1.0~1.0 사이의 값을 만들어줍니다. 그럼 이 값들을 shader 에 넣어서 확인해보겠습니다.

8-9 행에서 p 를 두 부분으로 나눴습니다. 일단 화면에는 첫번째 항의 p 계산 결과를 r, g 채널에 출력하고 있고, 화면이 전체적으로 노란색인 것으로 볼 때 예상대로 대부분의 값이 1 이상인 것을 알 수 있습니다. 9행의 주석을 해제해보면 화면 왼쪽과 아래쪽에 랜덤값이 주는 변화가 생기긴 하지만 여전히 화면은 전체적으로 노란색입니다.

12행의 주석을 해제해보면 화면이 그리드로 뒤덮인 것을 확인할 수 있습니다. sin 함수의 결과값답게 빨간색과 초록색이 규칙적으로 나타나며 1.0 이 출력되는 부분을 보여줍니다. 검은색 부분이 좀 더 많은 것은 음수 부분이 모두 0.0 과 같은 값으로 표시되기 때문입니다. 다시 9행의 주석을 해제해보면 랜덤값이 사라지고 일정한 그리드만 표시되는 것을 볼 수 있습니다.

그리고 r 값을 원래 for-loop 에서 변하는 값인 1.0 에서 4.0 까지 변화시키면 그리드가 점점 촘촘해지는 것을 볼 수 있습니다.

아직까지는 실마리가 잡히지 않습니다. 코드를 좀 더 봐야합니다.

// Current drop properties. Coordinates are rounded to ensure a
// consistent value among the fragment of a given drop.
vec4 d = texture(iChannel1, round(u * x - 0.25) / x);

round 는 반올림을 해주는 inline function 입니다만 three.js 의 fragment shader 에서 지원하지 않는 함수입니다. 대신에 floor(a+0.5) 를 사용하면 같은 효과를 낼 수 있습니다. 이 d 값을 shader 에 넣어보겠습니다.

uv 에 x 를 곱하면 x 는 큰 값이기 때문에 texture1 이 축소되어 작은 영역에 표시되고 다른 부분은 이미지를 쭉 늘린 것처럼 보이는 효과가 될 것입니다. 여기서 -0.25 를 해주면 원본 이미지가 오른쪽 위로 살짝 이동한 효과를 갖게 됩니다(8행 주석 해제). 그 다음 위에서 본 round 함수의 효과를 주기 위해 floor(uv * x - 0.25 + 0.5) 를 계산해주면 커다란 그리드가 생성됩니다(9행 주석 해제). 다만 오른쪽 위는 모두 같은 색깔이 표시되는데, 이는 floor 의 결과로 1.0 이상인 값이 나오고 있기 때문입니다. 이 문제를 방지하기 위해서 x 로 uv 를 나눠줍니다(10행 주석 해제).

어떤 실수에 x 를 곱한 다음에 floor 를 취하고 다시 x 로 나눠주면 0, 1, 2, ... , x-1 까지의 정수를 얻을 수 있습니다. 2차원에서 이 작업을 하면 그리드를 얻을 수 있습니다. 이렇게 그리드가 형성되면 그리드 안에서는 모두 같은 값을 갖게 됩니다.

사라지는 빗방울

빗방울을 계산하기 위한 기본적인 재료들을 앞에서 준비하는 과정이었다면, 뒷부분에서는 실제로 빗방울을 그려줍니다. 일단 첫번째로 t 를 계산하는데, 이것은 앞에서 계산한 s 의 s.x 와 s.y 를 더한 다음 복잡한 식에 곱해줍니다.

float t = (s.x+s.y) * max(0., 1. - fract(iTime * (d.b + .1) + d.g) * 2.);

복잡한 식은 max 로 최소 0. 값을 보장합니다. d 는 그리드였기 때문에, d.b 와 d.g 는 넓은 영역에서 일정한 값을 가질 것입니다. t 를 shader 로 나타내 보겠습니다.

time 이 들어가니 확실히 변화가 생겼습니다. 각 그리드에 빗방울 같은 것이 생겼다가 없어지는 것을 확인할 수 있습니다. time 은 d 에서 나온 값에 곱해지기 때문에, 각 그리드에서 빗방울은 동일한 시간동안 나타났다가 사라집니다. 각 빗방울의 모양은 다른데, 그 이유는 위에서 계산한 s 가 불규칙한 모양이기 때문입니다. 10행의 주석을 해제해보면 랜덤이 없어진 마름모꼴의 빗방울을 볼 수 있습니다.

여기서도 r 을 1.0~4.0 까지 변화시키며 그리드의 크기가 변하는 것을 확인할 수 있습니다. 그런데 p 에 곱해지는 6.28 을 변화시켜보면 그리드를 구성하는 빗방울의 크기가 달라지는 것을 확인할 수 있습니다. 오직 6.28 일 때만 그리드에 정확하게 맞는 빗방울이 생깁니다.

이것은 바로 sin 의 주기가 \(2 \pi\) 이기 때문입니다. 9행의 6.28 을 유지한 상태에서 12행의 주석을 해제해보면 빗방울이 정확하게 그리드에 반만 걸치는 것을 볼 수 있습니다. 12행은 sin 함수를 평행이동시키는 것이고, 9행 또는 10행의 6.28 을 바꾸는 것은 sin 의 주기를 바꾸는 것이 됩니다. 숫자가 작아지면 그리드의 크기가 커지고, 빗방울의 크기는 커지고 숫자는 적어집니다.

또 n 에 곱해지는 .1 을 1.0 으로 바꿔보거나 .01 로 바꿔보면 빗방울의 모양이 확실히 달라지는 것을 볼 수 있습니다. .1 은 랜덤 텍스처에서 얼마나 큰 영역을 사용하는지를 결정하는 수이기 때문에, 큰 영역을 사용하면 빗방울이 세밀해지고 작은 영역을 사용하면 랜덤값이 거의 사라지게 됩니다.

이제 우리는 빗방울의 형태를 파악했습니다. 코드에서는 이런 빗방울을 확률로 표시합니다.

// d.r -> only x% of drops are kept on, with x depending on the size of drops
if (d.r < (5.-r)*.08 && t > .5) {
    ...
}

첫번째 조건은 d.r < (5.-r) * .08 입니다. 위에서 그리드의 g, b 를 썼는데 이번에는 r 채널이 나왔습니다. 이 임의의 값이 (5.-r) * 0.8, 즉 r=1.0~4.0 일 때 0.32~0.8 이하여야 빗방울을 그려주려고 하는 것입니다. 위에서 확인한 것처럼 r 값이 작을수록 그리드가 커지고 빗방울도 커지는데, 출현할 확률은 그에 반비례해서 작아지게 됩니다.

두번째 조건은 t > .5 입니다. t 는 빗방울의 유지시간입니다. .5 보다 큰 값만 남기겠다는 이야기는 그 이하의 값일 때는 빗방울을 표시하지 않겠다는 것입니다. 빗방울이 서서히 작아지다가 일정 크기 이하일 때 순식간에 증발하는 것을 생각하면, 이것은 그럴듯한 구현입니다.

이 조건을 적용하고 for-loop 까지 돌려보면 좀 더 그럴듯한 빗방울 효과를 확인할 수 있습니다.

빗방울이 겹치면서 좀 더 멋진 효과를 보여주고 있습니다. 그리고 if 문의 첫번째 조건에 의해서 특정한 빗방울들만 표시됩니다.

그럼 이제 normal 에 대해서 알아볼 차례입니다.

// Drop normal
vec3 v = normalize(-vec3(cos(p), mix(.2, 2., t-.5)));
//fragColor = vec4(v * 0.5 + 0.5, 1.0);  // show normals

Shadertoy 불 쉐이더 분석에서 normal 이 무엇인지 간략하게 설명해 드렸습니다. normal 이란 물체의 중심에서 바깥쪽으로 향하는 표면의 방향 벡터입니다. 표면의 디테일을 추가해주는 용도로 쓰이며, 3D 효과를 낼 수 있습니다.

normalize 함수는 벡터를 정규화합니다. 즉 벡터의 각 구성요소를 벡터의 크기로 나눠줍니다.

v 의 처음 두 항인 x, y 는 -cos(p) 로 구합니다. 이렇게 되면 빗방울의 모양을 만들 때 구한 sin(p) 와 주기가 \(\frac{\pi}{2}\) 차이나게 됩니다.

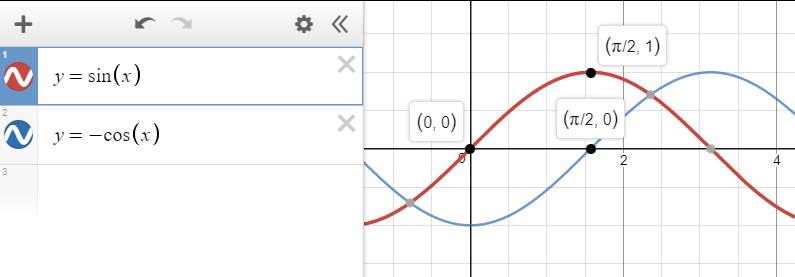
위에서 구했던 s 로 비교해보면 sin(p) 와 -cos(p) 를 넣었을 때 그리드의 위치가 서로 어긋나게 되는 것을 확인할 수 있습니다.

그러면 sin(p) 와 -cos(p) 는 실제로 어떤 관계가 있을까요? shader 에서 확인해보겠습니다.

sin(p) 값을 r, g 채널에 출력해보면 빗방울의 중앙부가 노란색이 됩니다. 즉 sin(p).xy 값이 1.0 에 가까운 max 값을 보이게 됩니다.

16행의 주석을 해제해보면 빗방울이 좀 더 입체적으로 보이는 것을 볼 수 있습니다. sin(p) 와 -cos(p) 는 그리드 상에서 서로 어긋나기 때문에, 값이 0.0 이 되는 검은색 부분도 존재하고 가운데를 중심으로 경계선이 뚜렷한 모습을 보입니다.

v 의 세번째 항인 z 는 mix(.2, 2., t-.5) 로 구합니다. The book of shaders 의 mix 를 참조하면, mix(a,b,c) 는 a 와 b 사이의 값을 c 만큼 보간해주는 값입니다. 즉 \((1-c) \times a + c \times b\) 가 됩니다. c 에는 보통 0.0~1.0 사이의 값이 들어가며 그 이하, 이상의 값은 clip 됩니다. 이 정의에 따르면 v.z 는 .2 에서 2.0 사이의 값을 가지고, t-.5 에 비례하게 됩니다. 다만 여기서 v.z 는 normalize 를 할 때만 쓰이고 다른 의미를 가지지는 않습니다. 물론 v.z 가 너무 커지면 v.x, v.y 가 그에 영향을 받아서 작아질 것이고, 반대의 경우는 커질 것입니다.

드디어 마지막 부분까지 왔습니다. 이렇게 구한 normal 으로 빗방울을 어떻게 출력할까요?

f = texture(iChannel0, u - v.xy * .3);

u 는 uv 입니다. 결국 uv 에서 normal.xy 의 .3 을 빼줍니다. 이렇게 간단한 구현으로 동작이 가능한 것인지 shader 에서 알아보겠습니다.

for-loop 바깥쪽에서는 mipmap 에 1.5 를 더한 배경 texture0 을 그려주고 있습니다. 그리고 for-loop 안에서 빗방울 효과를 적용하고 있습니다. 처음 세팅에서는 18행에서 빗방울 효과를 그려주고 있는데, 흐릿한 화면을 빗방울 영역만큼 선명하게 해주는 효과밖에 없습니다.

normal 을 적용하기 위해 19행의 주석을 해제해보면, 빗방울이 보이긴 하지만 뭔가 다 비슷한 모양입니다. 이것은 normal 의 적용 영역이 너무 넓기 때문입니다. 20행의 주석을 해제해보면 배경 texture0 전체 영역이 빗방울 하나에 들어가고 있는 것을 알 수 있습니다. 19행에서는 - 를 해줬기 때문에 뒤집혀 보였던 것이고, 20행에서는 + 를 해주고 있기 때문에 배경 화면이 빗방울에 온전하게 들어가 보입니다.

21행, 22행은 normal 에 .3 을 곱해서 이런 영향력을 제한하고 있습니다. 주석을 해제해보시고, 이 영역을 더 좁히거나 늘리면서 실험을 해보시기 바랍니다.

이것으로 빗방울 효과에 대한 글을 마치도록 하겠습니다. 긴 글을 읽어주셔서 감사합니다.