강화학습 알아보기(2) - DQN

01 Apr 2019 • 0 Comments Tags:

[ reinforcement-learning ]

가치 함수, 감가율
ball-find-3
Q 함수
DQN

가치 함수, 감가율

지난 글에서는 강화학습에 대해 처음으로 알아보는 시간과 함께 감가율(discount rate), 가치 함수(value function) 등의 개념을 소개했습니다. 두 개념을 다시 간략하게 정리하면 다음과 같습니다.

감가율 : 미래의 보상은 현재의 보상보다 가치가 낮기 때문에 보상에 미래 시점의 time step 만큼 곱해주는 0.0~1.0 사이의 실수 값
가치 함수 : 상태의 가치를 숫자로 표현한 것

가치 함수는 상태의 가치를 숫자로 표현하기 때문에, Grid World 위에 각 상태 공간에 대한 가치 함수를 구한 다음 가치 함수가 높은 곳으로 움직이는 단순한 방법으로 쉽게 해를 찾을 수 있다는 점을 같이 살펴보았습니다.

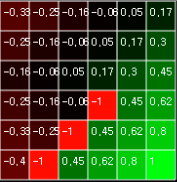그림 1. Grid World 의 각 상태에 대한 가치 함수 계산

가치 함수의 계산은 각 상태의 값이 변하지 않을 때까지 반복적으로 계산해서 결정되었습니다. 지난 글에서 다뤘던 Grid World 는 에이전트(agent) 를 제외한 다른 환경, 오브젝트나 목표의 위치는 고정되어 있었기 때문에 일단 가치 함수를 다 계산한 다음에 문제를 풀면 쉽게 풀 수 있었습니다.

하지만 여기에는 두 가지 문제가 있습니다. 첫째, 고정된 환경의 경우라고 해도 환경의 크기가 몹시 크면 가치 함수를 저장하는 메모리의 크기도 커져야 합니다. 우리가 다룬 환경은 6x6 이었기 때문에 가치 함수의 계산을 위해서는 36 의 길이를 가진 저장공간이 필요했지만 60x60 이라면 3,600 의 길이를 가진 저장공간이 필요할 것입니다. 둘째, 다이나믹한 환경에 대한 대응이 힘듭니다. 60x60 처럼 크기가 큰 환경일 때 가치함수를 계산하기 위해서는 여러 step 이 필요할 것입니다(그림 1 과 같은 결과를 얻기 위해서는 11 step 이 필요했습니다). 그런데 여기서 장애물이 움직이거나 목표가 움직인다면 매 step 마다 가치 함수의 계산을 다시 해줘야 합니다.

이 문제를 해결하기 위해서는 환경의 크기에 영향을 받지 않는 고정된 크기의 입력을 받으면 좋을 것입니다. 그리고 문제를 풀기 위한 더 효율적인 알고리즘을 사용해야 합니다.

ball-find-3

그럼 먼저 다이나믹한 환경에 해당되는 문제를 정의해 보겠습니다. ball-find-3 라는 이름을 붙인 이 Grid World 환경에서는 에이전트와 3개의 ball 이 랜덤한 위치에 생성됩니다. 에이전트가 ball 과 위치가 겹쳐질 때 ball 이 없어지며 +1.0 의 reward 를 받고, 3개의 ball 을 모두 없애거나 200 step 이 되면 하나의 episode 가 종료됩니다. 그리고 매 step 마다 -0.1 의 reward 를 받습니다. 에이전트가 선택할 수 있는 행동은 인접한 4방향으로 한 칸 이동하는 것입니다. 여기에 에이전트가 랜덤한 행동을 선택하는 ball-find-3 의 예가 있습니다.

let canvas = document.getElementById('editor_canvas_0');
canvas.width = 410;
canvas.height = 310;
removeClass(canvas, 'previewOutside');
addClass(canvas, 'previewOutside_410');
let ctx = canvas.getContext('2d');
let env = new Env(8, canvas);
env.maxEpisodes = 1000;
let agent = new Agent(env, Math.floor(Math.random() * 8), Math.floor(Math.random() * 8), canvas);
agent.ball_count = 3;
env.setEntity(agent, {'ball': 3});
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 410 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Step(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 410 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];

button.onclick = function() {
    if (is_running) return;
    iterate(false);
}

button2.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let action = Math.floor(Math.random() * 4);
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array.slice(rewards_array.length - 100), 255, 60);

            ctx.beginPath();
            ctx.fillStyle = 'limegreen';
            ctx.font = '14px monospace';
            let avg = rewards_array.reduce((acc, cur) => acc+cur, 0) / rewards_array.length;
            ctx.fillText(`avg. reward: ${Math.floor(avg * 10) / 10}`, env.grid_W * env.grid_width + 20, env.grid_W * env.grid_width + 60);
            ctx.closePath();
        }

        agent.x = Math.floor(Math.random() * 8);
        agent.y = Math.floor(Math.random() * 8);
        agent.reward = 0;
        agent.dir = 3;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        agent.ball_count = 3;
        while (true) {
            if (env.setEntity(agent, {'ball': 3}) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

Grid World 의 크기는 8x8 입니다. 이론적으로 최고점은 3번의 step 만에 ball 3개를 모두 획득하여 +2.7 의 reward 를 얻는 것이지만, 이렇게 배치 운이 좋은 경우는 드물 것이고, 보통은 양수나 -2.0 이상의 음수를 reward 로 얻게 된다면 좋은 성적이라고 할 수 있을 것 같습니다. 랜덤한 행동을 하는 에이전트를 1,000 episode 동안 실행시켜 보면 -14~-17 정도의 avg. reward 를 얻을 수 있습니다. 이를 기준으로 삼고 다양한 강화학습 알고리즘으로 avg. reward 를 개선해보도록 하겠습니다.

Q 함수

지난 글 에서 살펴보았던 가치 함수는 모든 상태 공간을 가치로 치환할 수 있었습니다. 가치 함수를 구한 다음 상태에 대한 가치 함수를 비교하고 가치가 높은 곳으로 움직이는 행동을 선택해서 해를 찾을 수 있었습니다.

이에 비해 Q 함수는 상태를 행동으로 치환하는 함수입니다. ball-find-3 의 에이전트는 인접한 4개 상태로 움직이는 상/하/좌/우 4방향의 이동 행동이 가능합니다. Q 함수는 각 상태에 대해서 이 행동의 값을 각각 구하고, 가장 높은 Q 값을 가진 행동을 선택해서 움직입니다. 이렇게 구하는 Q 함수를 정책(policy) 이라고도 합니다. Q 는 Quailty 의 약자로 특정 행동의 품질을 나타냅니다.¹

가치 함수는 수식으로 \(V(s)\)로 나타내고, Q 함수는 \(Q(s,a)\)로 나타냅니다. 여기서 s 는 state, a 는 action 을 의미합니다. 상태에만 의존하는 가치 함수와 달리 Q 함수는 상태와 행동에 의해 결정되는 값입니다.

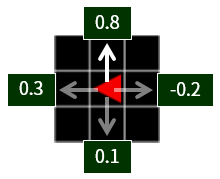그림 2. 이 위치(상태)에서 위쪽으로 한 칸 움직이는 행동은 Q 함수 값이 0.8 로 가장 큽니다. 에이전트는 Q 함수 값이 높은 행동을 무조건 선택하거나, 높은 확률로 선택합니다.

Q 함수의 값을 업데이트하기 위해서는 현재 가치와 미래 가치를 모두 고려해야 합니다. 현재 가치에 해당하는 부분은 지금 상태(s)에서 행동(a)을 취했을 때 Q 함수의 값입니다.

\[Q(s,a)\]

미래 가치에 해당하는 부분은 그 행동으로 인해 다음 상태(\(s'\))에 도달했을 때 취할 수 있는 행동(\(a'\))의 Q 함수 값입니다.

\[Q(s',a')\]

Q 함수의 실제 가치는 행동으로 얻는 보상을 빼놓고 생각할 수 없습니다. 보상을 R 이라고 한다면 Q 함수의 실제 가치는 보상에 미래 가치를 더한 식이 될 수 있습니다.

\[Q(s,a) \simeq R + Q(s',a')\]

\[실제 가치 \simeq 현재 가치 + 미래 가치\]

미래 가치에는 감가율이 적용된다고 했습니다. 따라서 이 식에 감가율을 적용하면 \(Q(s',a')\) 에 \(\gamma\) 가 곱해집니다.

\[Q(s,a) \simeq R + \gamma Q(s',a')\]

그런데 \(s'\) 상태에서 할 수 있는 \(a'\) 행동은 현재 Grid World 의 경우 4방향 이동, 4개입니다. 4개의 \(Q(s',a')\) 중 가장 큰 것, max 값을 구한다고 생각하면 식을 좀 더 정리할 수 있습니다.

\[Q(s,a) \simeq R + \gamma maxQ(s',a')\]

이제 어느 정도 윤곽이 보입니다. 목표는 \(Q(s,a)\) 값이 \(R + \gamma maxQ(s',a')\) 에 가까워지도록 하는 것입니다. 즉 강화학습을 통해서 \(Q(s,a)\) 를 업데이트 하는 것입니다. 반복 시행으로 여러 개의 값을 얻은 후 평균(average)을 내는 것이 가장 쉽게 생각할 수 있는 방법입니다. 어떤 값의 평균은 전체 데이터를 데이터 개수로 나눠서 구할 수 있습니다. 예를 들어 n-1 개의 수가 있을 때 평균은 아래와 같은 식으로 구할 수 있습니다.

\[average = \frac{1}{n-1} \sum_{i=1}^{n-1} A_{i}\]

새로운 값이 더해진 후 다시 평균을 구하려고 할 때, 기존의 값을 모두 더한 뒤에 다시 데이터 개수로 나누는 방법도 있지만, 다음과 같은 식으로 변형시킬 수도 있습니다.

\[\begin{align} average' & = \frac{1}{n} \left(\sum_{i=1}^{n-1} A_{i} + A_{n} \right) \\ & = \frac{1}{n} \left((n-1) \times \frac{1}{n-1} \sum_{i=1}^{n-1} A_{i} + A_{n} \right) \\ & = \frac{1}{n} ((n-1) \times average + A_{n}) \\ & = \frac{n-1}{n} \times average + \frac{A_{n}}{n} \\ & = average + \frac{1}{n} (A_{n} - average) \end{align}\]

평균을 구하는 식이 이전 평균에 새로운 값과 이전 평균의 차이를 n으로 나눈 값을 더하는 것으로 바뀌었습니다. 이때 \(\frac{1}{n}\) 은 시행 횟수가 많아질수록 점점 작아질 것입니다. 이것을 일정한 크기의 숫자인 \(\alpha=0.1\) 등으로 바꿀 수 있습니다. 이 \(\alpha\) 를 학습률(learning rate)이라고 합니다. 이 값을 시행 횟수에 따라 늘어나거나 줄어들도록 조절해서 학습이 잘되는 방향으로 이끌 수 있습니다.

\[average' = average + \alpha(A_{n} - average)\]

지금까지 정리한 식을 Q 함수를 구하는 데에 도입해 보겠습니다. 기본적인 형태는 같고, \(\frac{1}{n}\) 이 \(\alpha\) 로, average 가 \(Q(s,a)\) 로, 새로운 값인 \(A_{n}\) 이 \(R + \gamma maxQ(s',a')\) 가 되었습니다.

\[Q(s, a) = Q(s, a) + \alpha (R + \gamma max Q(s',a') - Q(s,a))\]

그럼 이제 가치 함수처럼 고정된 환경에서 Q 함수를 구해보겠습니다. 원활한 계산을 위해 ball-find-3 가 아닌 지난 글 에서 살펴봤던 구덩이가 있는 환경을 다시 사용하겠습니다. 에이전트의 위치는 (x=0,y=0) 으로 고정되어 있고, 목표의 위치와 구덩이의 위치도 고정되어 있습니다.

지난 글 에서 살펴봤던 가치 함수를 구할 때처럼 모든 상태, 모든 행동에 대한 Q 함수를 구할 것입니다. 처음에는 값이 없기 때문에 모두 0 으로 초기화합니다.

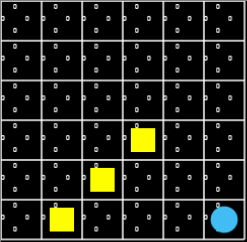그림 3. 구덩이 3개와 목표 1개가 고정된 위치에 있는 환경. 각 상태, 각 행동의 Q 함수는 모두 0으로 초기화합니다.

가치 함수와 달리 Q 함수는 에이전트의 탐색에 따라 테이블의 빈 칸을 채워넣게 됩니다. 에이전트는 기본적으로 Q 값이 높은 행동을 선택하지만, 이로 인해 충분히 탐색하지 않고 ‘적당히 좋은’ 해결책을 찾아내면 그것에 수렴해버리는 문제가 발생합니다. 이를 방지하기 위해 \(\epsilon\)(epsilon)-greedy 방법이라는 탐색법을 사용합니다. \(\epsilon\) 이란 매우 작은 숫자입니다. 0.0~1.0 사이의 랜덤한 수와 이 \(\epsilon\) 을 비교하여, \(\epsilon\) 이 더 크면 무작위 행동을 반환하고, 그렇지 않으면 Q 함수에 따라서 움직이게 됩니다. 즉 \(\epsilon\) 이 0.3 이라면 30% 의 확률로 무작위 행동을 선택하게 되는 것입니다.

IF randomNumber < epsilon:
    getRandomAction()
ELSE:
    getGreedyAction() // by Q

\(\epsilon\) 은 0.0~1.0 사이의 값을 사용하고, 보통 탐색이 진행됨에 따라 값을 서서히 낮춥니다(cf. 시작값은 0.3, episode 가 끝날 때마다 0.99 를 곱함. 최소값은 0.01). 이를 epsilon decay 라고 합니다.

let canvas = document.getElementById('editor_canvas_1');
canvas.width = 410;
canvas.height = 310;
removeClass(canvas, 'previewOutside');
addClass(canvas, 'previewOutside_410');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
env.grid_width = 40;
env.maxEpisodes = 200;
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1, 'box': 3}, [[5, 5], [3, 3], [2, 4], [1, 5]]);

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 410 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Step';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 410 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Loop';
canvas.parentNode.appendChild(button2);

let q_array = new Array(env.grid_W * env.grid_W * 4).fill(0);
let initial_policy_obj = {};
let idx;
for (let d = 0; d < 4; d++) {
    for (let y = 0; y < env.height; y++) {
        for (let x = 0; x < env.width; x++) {
            idx = d + x * 4 + y * 4 * env.grid_W;
            q_array[idx] = 0.0;
            initial_policy_obj[idx.toString()] = 0.0;
        }
    }
}

const gamma = 0.9;
const learning_rate = 0.1;
let epsilon = 0.3;
let epsilon_min = 0.0;
let epsilon_multiply = 0.99;

drawPolicy();
env.draw();

function drawPolicy() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y, d, m;
    for (let i = 0; i < q_array.length; i += 1) {
        x = Math.floor(i / 4) % env.grid_W;
        y = Math.floor(i / (env.grid_W * 4));
        d = i % 4;

        // not empty - not draw
        if (env.grid[y][x].length !== 0) {
            continue;
        }

        ctx.beginPath();

        if (i % 4 === 0) {
            m = Math.max(...q_array.slice(i, i+4));
        }

        if (q_array[i] === m) {
            ctx.strokeStyle = 'yellow';
            ctx.lineWidth = 2;
        }

        if (q_array[i] >= 0.0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(q_array[i] * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor(Math.min(Math.abs(q_array[i]), 1.0) * 255)}, 0, 0)`;
        }


        ctx.moveTo((x + 0.5) * env.grid_width, (y + 0.5) * env.grid_width);
        ctx.lineTo((x + dirs_tri[d][0][0]) * env.grid_width, (y + dirs_tri[d][0][1]) * env.grid_width);
        ctx.lineTo((x + dirs_tri[d][1][0]) * env.grid_width, (y + dirs_tri[d][1][1]) * env.grid_width);
        ctx.lineTo((x + 0.5) * env.grid_width, (y + 0.5) * env.grid_width);
        ctx.fill();

        if (q_array[i] === m) {
            ctx.stroke();
        }

        //ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '7px monospace';
    for (let i = 0; i < q_array.length; i += 1) {
        x = Math.floor(i / 4) % env.grid_W;
        y = Math.floor(i / (env.grid_W * 4));
        d = i % 4;

        // not empty - not draw
        if (env.grid[y][x].length !== 0) {
            continue;
        }

        ctx.fillText(q_array[i], (x+0.5+dirs[d][0] * 0.3) * env.grid_width - 8, (y+0.5+dirs[d][1] * 0.3) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

button.onclick = function() {
    iterate(false);
}

button2.onclick = function() {
    iterate(true);
}

let is_running = false;
let rewards_array = [];

function iterate(is_loop = true) {
    let q_s = [];
    let x, y, state_idx;
    state_idx = (agent.x + agent.y * env.grid_W) * 4;
    q_s = q_array.slice(state_idx, state_idx + 4);

    // find max q
    const m = Math.max(...q_s);
    q_s = q_s.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
    let action;

    // epsilon-greedy
    if (Math.random() < epsilon) {
        action = Math.floor(Math.random() * 4);
    }
    else {
        action = q_s[Math.floor(Math.random() * q_s.length)];
    }

    let reward, done;
    [reward, done] = agent.step(action);
    let next_state_idx = (agent.x + agent.y * env.grid_W) * 4;

    // update q
    q_array[state_idx + action] += learning_rate * (reward + gamma * Math.max(...q_array.slice(next_state_idx, next_state_idx + 4)) - q_array[state_idx + action]);

    q_array[state_idx + action] = Math.floor(q_array[state_idx + action] * 100) / 100;

    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawPolicy();
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 255, 80);

            ctx.beginPath();
            ctx.fillStyle = 'white';
            ctx.font = '14px monospace';
            ctx.fillText(`epsilon: ${epsilon}`, env.grid_W * env.grid_width + 20, env.grid_W * env.grid_width + 40);
            ctx.closePath();
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        // epsilon_decay
        if (epsilon > epsilon_min) {
            epsilon = epsilon * epsilon_multiply;
            epsilon = Math.floor(epsilon * 10000) / 10000;
        }

        while (true) {
            if (env.setEntity(agent, {'ball': 1, 'box': 3}, [[5, 5], [3, 3], [2, 4], [1, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

// because of mathjax.. reset position
var el = document;
var event = document.createEvent('HTMLEvents');
event.initEvent('resize', true, false);
setTimeout(function() {el.dispatchEvent(event);}, 1000);

Step 버튼을 누르면 에이전트가 1 step 움직이고, Loop 버튼을 누르면 에이전트가 maxEpisode 에 도달할 때까지 자동으로 계속 움직입니다.

Q 함수의 값은 시간이 지날수록 업데이트되며, 목표에 가까운 상태에서 목표에 도달하는 행동을 하는 Q 값은 초록색(양수)으로 변하고, 구덩이 옆에 있는 값은 빨간색(음수)으로 변합니다. 노란색 삼각형은 각 상태에서 max 에 해당되는 Q 함수의 값을 의미합니다. 대략 100 episode 이후에는 epsilon 값도 낮아지고 Q 함수의 최적해를 찾게 되어 거의 헤매지 않고 목표에 도달합니다.

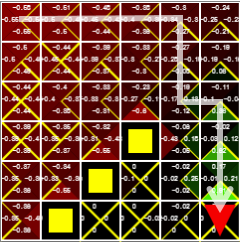그림 4. 각 상태의 max Q 값을 의미하는 노란색 삼각형을 따라가면 목표에 도달할 수 있습니다.

고정된 상태에서는 이렇게 Q 함수의 값, 즉 \(상태(s) \times 행동(a)\) 크기의 Q 테이블을 채워서 최적해를 찾을 수 있습니다. 위의 Grid World 에서는 \(36 \times 4 = 144\) 가 될 것입니다. 그런데 앞에서 고려했던 환경의 크기가 몹시 큰 경우에는 어떻게 대응해야 할까요?

먼저 환경의 크기가 얼마나 커지든 입력의 크기가 일정해야 한다는 기본 전제가 필요합니다. 그렇지 않고 환경의 모든 상태를 고려하게 된다면 행동의 계산에 필요한 메모리가 환경의 크기에 비례해서 늘어나게 될 것입니다.

로봇 등으로 학습시키는 실제 환경에서도 주변을 감지하는 센서의 범위는 한정적인 것처럼, 에이전트의 시야를 임의로 제한하여 시야 내의 영역의 정보만 입력으로 받아서 판단하게 할 수 있습니다.

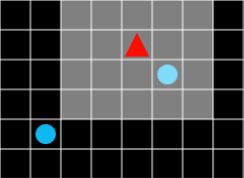그림 5. 시야 범위는 밝게 표시합니다.

이렇게 될 때 각 상태는 시야 범위에 들어온 모든 오브젝트의 현상황이 됩니다. 에이전트가 어떤 셀에 위치해 있는지 뿐만이 아니라, 에이전트의 시야에 어떤 풍경이 보이는지도 상태값에 영향을 끼칩니다. 풍경에 보이는 것이 조금만 달라져도 상태값은 달라져야 합니다. 즉 상태 메모리의 크기는 시야의 크기에 비례하는 것이 아니라 기하급수적으로 증가할 수 있습니다.

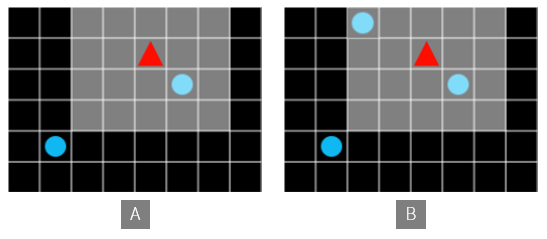그림 6. A 와 B 는 다른 상태로 취급됩니다.

따라서 위에서 했던 방법처럼 Q 함수를 테이블로 저장할 수는 없습니다. 많은 양의 데이터를 효과적으로 저장하고, 그 데이터를 효율적인 함수 출력으로 바꾸는 신경망 네트워크를 쓰는 것을 하나의 방법으로 생각해볼 수 있습니다. 이 지점에서 DQN 이 나왔습니다.

DQN

Deepmind 의 역사적인 논문인 “Playing Atari with Deep Reinforcement Learning”에서 Q 함수를 이용한 Q-Learning 에 Deep Neural Network 를 결합하여 Atari 2600 의 고전 게임을 성공적으로 플레이하는 에이전트를 발표했습니다. 특히 몇몇 게임에서 DQN 은 인간 고수의 플레이를 능가하는 점수를 획득했기 때문에 더욱 화제가 되었습니다.

그림 7. DQN 으로 학습한 에이전트가 Atari-breakout 을 플레이하고 있습니다. 스스로 학습하여 공을 블록 라인 뒤쪽으로 보내는 최적의 해를 찾아냅니다. 이미지 출처 링크

이 알고리즘은 연속된 4프레임에 해당하는 게임 화면을 Convolution 네트워크의 입력으로 받은 다음에, Q-Learning 학습 과정을 거쳐서 보상을 최대화하는 Q 함수를 학습했습니다. 사람이 게임을 플레이하는 것처럼, 에이전트는 주어진 화면을 보고 알맞은 키 조작을 통해 게임을 플레이하게 됩니다.

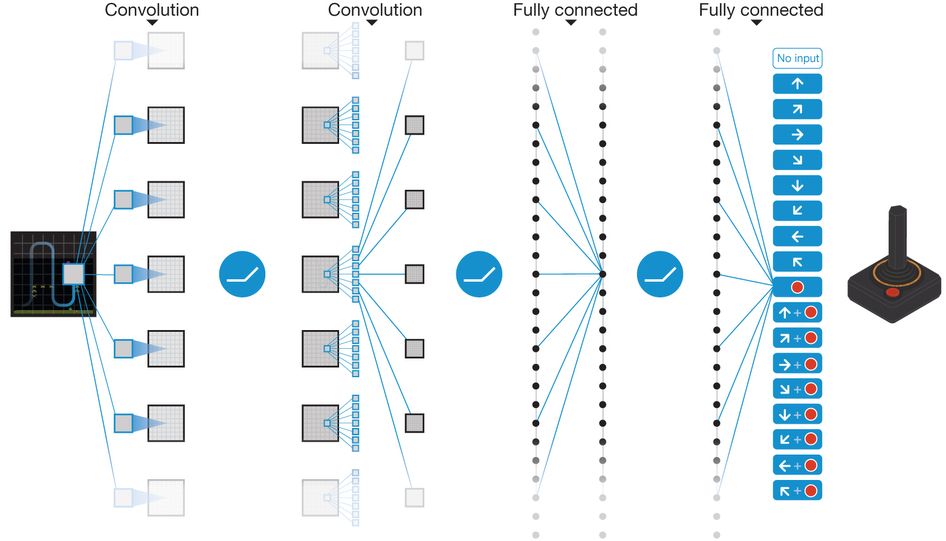그림 8. DQN 의 개략적인 네트워크 구조도입니다. 이미지 출처 링크

위의 고정된 환경의 Q-Learning 에서는 Q 테이블을 통해 상태를 행동으로 치환했다면, DQN 에서는 Q 네트워크를 통해 상태를 행동으로 치환하게 됩니다. 딥러닝 네트워크는 기존의 테이블 방식의 한계였던 메모리의 크기를 극복하고, 많은 양의 데이터에 대해 효율적인 함수 출력을 학습할 수 있습니다.

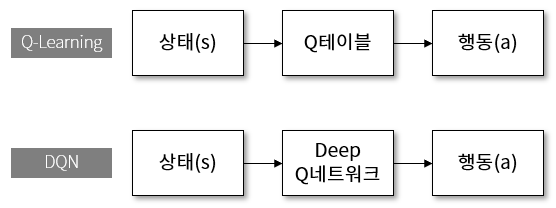그림 9. DQN 은 Deep Q-Network 의 약자입니다.

DQN 논문에는 Q 함수의 테이블을 네트워크로 치환한다는 기본적인 아이디어 외에도 성능을 높이기 위한 experience replay, target network 같은 아이디어들이 적용되어 있습니다. 이것들에 대해 자세히 설명드리는 것은 이 글에서 다루려는 내용을 벗어나는 일인 것 같아서, 관심이 있는 분들은 이 글을 참고하시면 도움이 될 것 같습니다.

여기서는 Grid World 환경에서 DQN 을 구현해보도록 하겠습니다. 딥러닝 라이브러리는 tensorflow-js 를 사용하였습니다. tensorflow-js 는 현재 전세계적으로 가장 널리 쓰이는 딥러닝 프레임워크인 tensorflow 의 javascript 버전으로, tensorflow 와 model 이 호환되며 keras 에 영향을 받은 간결한 API 사용을 지원합니다.

네트워크 구조는 그림 8에 비해 간단합니다. 에이전트의 시야에 해당하는 입력을 받은 다음 convolution layer 를 이용해서 이미지 정보를 압축하고 특징(feature)을 잡아냅니다. 그 다음 dense layer 를 연결하고 마지막에 액션의 크기와 같은 4개의 노드를 가진 dense layer 를 연결해서, 네트워크의 출력을 에이전트의 행동으로 사용합니다.

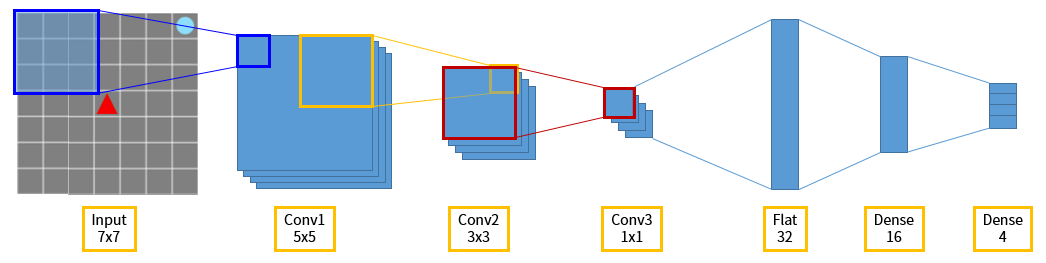그림 10. Grid World - DQN 에이전트의 네트워크 구조도

let global_step = 0;
let canvas = document.getElementById('editor_canvas_2');
canvas.width = 410;
canvas.height = 310;
removeClass(canvas, 'previewOutside');
addClass(canvas, 'previewOutside_410');
let ctx = canvas.getContext('2d');
let env = new Env(8, canvas);
env.maxEpisodes = 2000;
let agent = new DQNAgent(env, Math.floor(Math.random() * 8), Math.floor(Math.random() * 8), canvas);
agent.ball_count = 3;
agent.vision = true;
env.setEntity(agent, {'ball': 3});
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 410 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Learn(DQN)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 410 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Run(DQN)';
button2.disabled = true;
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];

let epsilon = 0.3;
let epsilon_min = 0.0;
let epsilon_multiply = 0.99;

button.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

button2.onclick = function() {
    if (is_running) return;
    is_running = true;
    env.maxEpisodes += 1;

    agent.x = Math.floor(Math.random() * 8);
    agent.y = Math.floor(Math.random() * 8);
    agent.reward = 0;
    agent.dir = 3;

    // env.episodes += 1;
    env.steps = 0;
    env.reset();

    agent.ball_count = 3;
    while (true) {
        if (env.setEntity(agent, {'ball': 3}) !== null) {
            break;
        }
    }

    run();
}

function getAction(agent, input) {
    if (Math.random() < epsilon) {
        return Math.floor(Math.random() * 4);
    }
    return tf.tidy(() => {
        let inputTensor = tf.tensor4d(input, [1, 7, 7, 1]);
        //const logits = agent.model.predict(inputs.reshape([1, 7, 7, 1]));
        const logits = agent.model.predict(inputTensor);
        const softmax = logits.softmax();
        const actions = tf.multinomial(softmax, 1, null, true);
        return actions.dataSync()[0];
    });
}

function getVision(agent) {
    let top, left;
    left = agent.x - agent.visionForward;
    top = agent.y - agent.visionForward;
    let s = [];

    for (let y = top; y < top + agent.visionForward * 2 + 1; y += 1) {
        for (let x = left; x < left + agent.visionForward * 2 + 1; x += 1) {
            if (x >= 0 && x < env.width &&
                y >= 0 && y < env.height) {
                if (env.grid[y][x].length > 0) {
                    s.push(object_to_idx[env.grid[y][x][0].type]);
                }
                else {
                    s.push(object_to_idx['empty']);
                }
            }
            else {
                s.push(object_to_idx['unseen']);
            }
        }
    }

    return s;
}

function run(is_loop = true) {
    const state = getVision(agent);
    const action = getAction(agent, state);
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));

    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    env.draw();
    agent.draw();

    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array.slice(rewards_array.length - 100), 255, 60);

            ctx.beginPath();
            ctx.fillStyle = 'limegreen';
            ctx.font = '14px monospace';
            let avg = rewards_array.reduce((acc, cur) => acc+cur, 0) / rewards_array.length;
            ctx.fillText(`avg. reward: ${Math.floor(avg * 10) / 10}`, env.grid_W * env.grid_width + 20, env.grid_W * env.grid_width + 60);
            ctx.closePath();
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

async function iterate(is_loop = true) {
    const state = getVision(agent);
    const action = getAction(agent, state);
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    const next_state = getVision(agent);
    agent.append_sample(state, action, reward, next_state, done);

    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    env.draw();
    agent.draw();

    global_step += 1;
    if (global_step % agent.learn_step === 0) {
        // if (agent.memory.getLength() >= agent.train_start) {
        if (agent.memory.length >= agent.train_start) {
            await agent.train_model();
        }
    }

    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array.slice(rewards_array.length - 100), 255, 60);

            ctx.beginPath();
            ctx.fillStyle = 'white';
            ctx.font = '14px monospace';
            ctx.fillText(`epsilon: ${epsilon}`, env.grid_W * env.grid_width + 20, env.grid_W * env.grid_width + 40);
            ctx.closePath();

            ctx.beginPath();
            ctx.fillStyle = 'limegreen';
            ctx.font = '14px monospace';
            let avg = rewards_array.reduce((acc, cur) => acc+cur, 0) / rewards_array.length;
            ctx.fillText(`avg. reward: ${Math.floor(avg * 10) / 10}`, env.grid_W * env.grid_width + 20, env.grid_W * env.grid_width + 60);
            ctx.closePath();
        }

        agent.x = Math.floor(Math.random() * 8);
        agent.y = Math.floor(Math.random() * 8);
        agent.reward = 0;
        agent.dir = 3;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        // epsilon_decay
        if (epsilon > epsilon_min) {
            epsilon = epsilon * epsilon_multiply;
            epsilon = Math.floor(epsilon * 10000) / 10000;
        }

        await agent.update_target_model();

        agent.ball_count = 3;
        while (true) {
            if (env.setEntity(agent, {'ball': 3}) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
    else {
        button.disabled = true;
        button2.disabled = false;
        is_running = false;
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

Learn(DQN) 버튼을 누르면 에이전트가 학습을 시작합니다. experience replay 가 적용되어 있기 때문에 에이전트는 경험하는 모든 정보를 (state, action, reward, next_state, done) 의 형태로 메모리에 저장하고, 일정 수(여기서는 1,000 개(train_start))의 정보가 쌓였을 때부터 학습을 시작합니다. 10 step(learn_step) 이 지날 때마다 메모리에서 뽑아낸 64개(batch_size)의 샘플을 이용해서 학습합니다.

2000 episodes 까지 학습했을 때 avg.reward 는 -11~-12 정도가 나옵니다. 랜덤액션 에이전트의 -14~-17 보다는 개선된 결과입니다. 딥러닝의 하이퍼파라미터 - train_start, learn_step, batch_size 등을 조절해보며 더 좋은 avg. reward 를 얻기 위해 노력해볼 수 있습니다. 또 네트워크 구조를 수정하거나 더 발전된 알고리즘(A2C, PPO 등)을 적용해서 avg. reward 를 높일 수 있습니다.

시야를 제한시킨 상태에서, 에이전트와 ball 이 임의의 위치에 생성되는 비교적 어려운 문제에서 DQN 에이전트가 랜덤액션 에이전트에 비해서 좋은 성적을 거둘 수 있다는 것을 확인했습니다. 하지만 아직 공을 보고 일직선으로 찾아가는 경우와 다른 쪽으로 가서 헤매는 비율이 비슷하게 보이는 것 같습니다. 다음 시간에는 이 에이전트의 효율을 더 높이는 방법에 대한 설명과, 더 어려운 문제를 풀 수 있는 더 효율적인 알고리즘을 설명드리도록 하겠습니다. 긴 글 읽어주셔서 감사합니다.

딥 강화학습 쉽게 이해하기(번역) ↩

greentec's blog game designer, scripter, researcher

강화학습 알아보기(2) - DQN

가치 함수, 감가율

ball-find-3

Q 함수

DQN

Related Posts

Shadertoy 'Bleepy blocks' 분석 03 May 2021

『시작하세요! 텐서플로 2.0 프로그래밍』 재고 추적 자동화 01 Mar 2020

『시작하세요! 텐서플로 2.0 프로그래밍』 집필 후기 18 Jan 2020