강화학습 알아보기(3) - DQN 개선, Deep SARSA

16 Apr 2019 • 0 Comments

• DQN 성능 끌어올리기
  • 하이퍼 파라미터 조정
  • weight initialization
  • soft update (target network)
  • Double DQN
  • Dueling DQN
• Deep SARSA

지난 글에서는 Deepmind 에서 개발하여 Atari 게임을 플레이하는데 사용되었던 DQN 을 Grid World 에서 학습시켜 보았습니다. 랜덤 액션 에이전트가 -14~-17 정도의 avg. reward 를 얻은 데 비해 DQN 에이전트는 -11~-12 정도의 avg. reward 를 얻었습니다.

하지만 이렇게 학습시킨 에이전트를 Run 버튼을 눌러서 움직여보면 목표 앞에서 헤매는 등 만족스러운 움직임을 보여주지는 못합니다. 오늘은 DQN 이 2013 년에 처음 발표된 후, 성능을 끌어올리기 위해 나왔던 여러 방법들을 적용해서 Grid World 에서 ball-find-3 문제의 avg. reward 를 높여보도록 하겠습니다. 그리고 이 문제를 풀기 위한 더 효율적인 알고리즘을 소개해 보겠습니다.

 

DQN 성능 끌어올리기

하이퍼 파라미터 조정

생각할 수 있는 가장 쉬운 방법은 하이퍼 파라미터(hyperparameter)를 조정하는 방법입니다. 하이퍼 파라미터란 딥러닝 네트워크의 학습에 영향을 미치는 학습률(learning rate), 배치 사이즈, 또 DQN 에 특화된 것으로 경험을 저장할 메모리의 전체 크기, 학습을 시작할 수 있는 메모리 사이즈, 감가율(discount rate, \(\gamma\)) 등이 있겠습니다.

그림 1. 하이퍼 파라미터 조정은 수많은 스위치를 조절해서 원하는 결과를 얻는 과정에 비유할 수 있습니다. 이미지 링크

이 중 learn_step 을 조정해볼 수 있습니다. 지난 글의 DQN 에이전트는 learn_step=10 으로, 10 step 마다 학습을 했습니다. 이 step 을 줄여보면 어떨까요? 당연히 에이전트는 좀 더 자주 학습하게 됩니다. 자주 학습하게 되면 avg. reward 도 높아질까요? learn_step=1 로 줄이면 에이전트는 1 step 마다 학습을 하게 되어 10 배 빠르게 학습할 것입니다.

weight initialization

딥러닝 네트워크는 수많은 실수(float) 값 가중치(weight)와 편향(bias)들로 구성됩니다. 이 값들이 딥러닝의 출력을 결정하지만 학습을 시작하기 전에는 이 값들이 정해지지 않은 상태이기 때문에 초기화 과정이 필요합니다. 보통 많이 쓰이는 방법은 랜덤한 수로 초기화하는 것이지만, Glorot Initialization 이라는 방법을 사용하면 좀 더 안정적인 결과를 내는 가중치의 초기값을 만들 수 있습니다. 이 방법은 Xavier Glorot 이라는 사람이 제안했기 때문에 Xavier Initialization 이라고도 불립니다.¹

soft update (target network)

지난 글에서 잠깐 설명드렸지만 DQN 에는 target network 라는 아이디어가 적용되어 있습니다. Q-Learning 에서 Q 값을 업데이트 하는 식을 다시 살펴보면 아래와 같습니다.

\[Q(s, a) = Q(s, a) + \alpha (R + \gamma max Q(s', a') - Q(s, a))\]

여기서 \(\alpha\) 는 학습률입니다. 업데이트 식에서 \(Q(s, a)\) 는 \(R + \gamma max Q(s', a') - Q(s, a)\) 에 \(\alpha\) 를 곱한 만큼 업데이트됩니다. \(\alpha=0\) 이라면 \(Q(s, a)\) 는 변하지 않을 것이고, \(\alpha=1\) 이라면 \(Q(s, a)\) 는 \(R + \gamma max Q(s',a')\) 가 될 것입니다. 보통 \(\alpha\) 는 0.0~1.0 사이의 값이기 때문에 이 업데이트 식은 다음과 같은 관계를 나타낸다고 생각할 수 있습니다.

\[Q(s, a) = Q(s, a) + \alpha (\underbrace{R + \gamma max Q(s', a')}_{target} - Q(s, a))\] \[Q(s, a) \rightarrow R + \gamma max Q(s', a')\]

즉 학습을 계속할 때 \(Q(s, a)\) 는 \(R + \gamma max Q(s', a')\) 에 가까워집니다. 여기서 Q-network 의 가중치와 편향을 \(\theta\) 로 표시한다면 위 식을 다음과 같이 쓸 수 있습니다.

\[Q(s, a;\theta) \rightarrow R + \gamma max Q(s', a';\theta)\]

이 식의 문제점은 현재 값과 목표가 같은 네트워크 가중치를 사용한다는 것입니다. 학습할 때마다 Q-network 의 가중치는 변하게 되는데, 목표도 같이 변하기 때문에 일정한 값으로 수렴하는 데에 어려움이 있을 수 있습니다. 따라서 target network 라는 Q-network 와 구조가 동일한 별도의 네트워크를 만들고, \(\theta^{-}\) 라는 기호로 표시합니다.

\[Q(s, a;\theta) \rightarrow R + \gamma max Q(s', a';\theta^{-})\]

그리고 target network 는 원래의 Q-network 가 몇 번 정도 학습하는 동안² 고정된 값을 유지하고 있다가, 주기적으로 원래의 Q-네트워크 값으로 리셋해줍니다. 이렇게 되면 고정된 target network 로 Q-network 가 가까워질 수 있기 때문에 효과적인 학습이 될 수 있습니다.

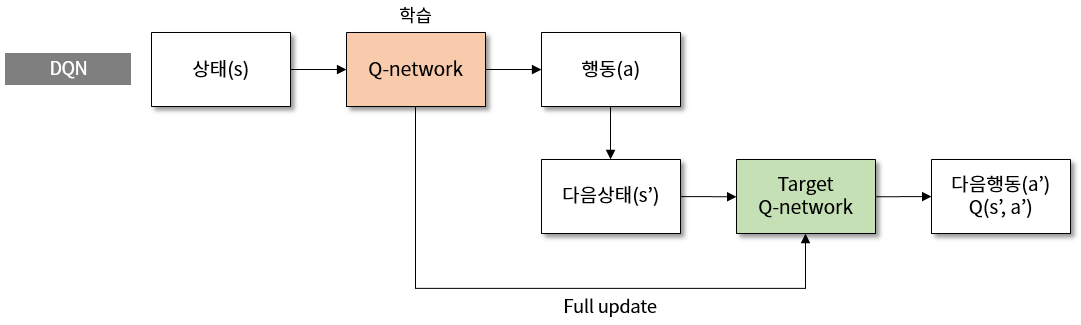그림 2. DQN 에서 target network 를 이용한 학습의 구조도

soft update 는 이 target network 의 update 를 한번에 하는 것이 아니라, 빈번하게 조금씩 하겠다는 의미입니다. \(\tau\) 라는 값을 사용하는데, DPG 라는 알고리즘을 제안한 Deepmind 의 논문³에서는 \(\tau=0.001\) 을 사용했습니다. target network 는 아래와 같은 식으로 업데이트 됩니다.

\[\theta^{-} = \theta \times \tau + \theta^{-} \times (1 - \tau)\]

target network 는 Q-network 의 값으로 아주 조금씩 이동하게 됩니다. \(\tau\) 값이 작기 때문에 업데이트는 빈번해야 영향이 눈에 보일 것입니다. 원래 episode 가 끝날 때마다 한번씩 target network 를 업데이트하던 것을, 학습할 때마다 soft update 하도록 코드를 수정해서 적용했습니다.

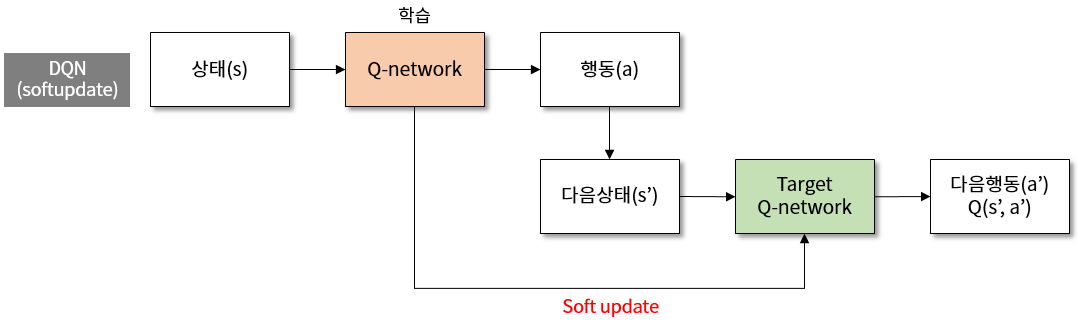그림 3. DQN 에서 target network 를 soft update 하는 학습의 구조도

그럼 위의 세 가지, learn_step 조정 + soft update(target network) + weight initialization(glorot initialization) 을 적용한 에이전트를 실험해보도록 하겠습니다.

Learn(DQN) 버튼을 눌러서 2000 episode 까지 여러 변경이 적용된 DQN 알고리즘을 돌려보면 -9~-10 정도의 avg. reward 를 얻을 수 있습니다. 순수한 DQN의 -11~-12 보다는 조금 개선된 결과입니다.

 

 

Double DQN

Deepmind 의 David Silver 는 “Deep Reinforcement Learning” 이라는 강연⁴에서 Nature 에 발표했던 DQN 이후의 주요 개선점으로 3가지를 꼽았습니다. 바로 Double DQN, Prioritized replay, Dueling DQN 입니다. 이 중 직접적인 계산에 변화가 있는 Double DQN 과 Dueling DQN 에 대해서 알아보겠습니다.

Double DQN 은 원래 DQN 이 나오기 전인 2010년에 Q-Learning 의 문제점을 개선하기 위해서 2 개의 Q-network 를 사용하는 방향의 알고리즘이었습니다. Hado van Hasselt 의 “Double Q-Learning” 논문에서는 Q 값이 과대평가(overestimation) 되는 경향이 있기 때문에 Q-Learning 이 잘 되지 않는 경우가 있다고 지적했습니다.

\[Q(s, a) = Q(s, a) + \alpha (R + \gamma max Q(s', a') - Q(s, a))\]

원래 Q-Learning 식에서 \(max Q(s', a')\) 를 뜯어보면 이 값은 상태 \(s'\) 가 주어졌을 때 Q-network 에서 가장 Q 값이 높은 \(a'\) 를 선택한 다음, 그 Q 값을 \(\gamma\) 에 곱해줘서 \(Q(s, a)\) 가 가까워져야 할 목표값을 만드는 것을 알 수 있습니다. 그런데 문제는 1. 선택, 2. Q값 가져오기 에서 동일한 Q-network 를 사용한다는 것입니다. max 연산을 사용하기 때문에 선택된 Q 값은 보통 큰 값이고, 그 값을 가져오기 때문에 Q 값은 점점 커지는 방향으로 가게 됩니다. 그런데 필요 이상으로 Q 값이 커지게 될 경우 Q-network 의 성능은 몹시 떨어지게 됩니다.

이를 방지하기 위해 Hado van Hasselt 가 처음 제시한 방법은 2개의 Q-network 를 사용하는 것입니다.

\[Q_{A}(s, a) = Q_{A}(s, a) + \alpha (R + \gamma Q_{B}(s', argmaxQ_{A}(s',a')) - Q_{A}(s, a))\] \[Q_{B}(s, a) = Q_{B}(s, a) + \alpha (R + \gamma Q_{A}(s', argmaxQ_{B}(s',a')) - Q_{B}(s, a))\]

두 식은 A, B 를 바꾸면 동일합니다. 위의 식을 기준으로 설명하면, \(argmaxQ_{A}(s',a')\) 부분이 \(Q_{A}\) 네트워크에서 행동을 선택하는 부분입니다. 그리고 바깥쪽의 \(Q_{B}(s', argmaxQ_{A}(s',a'))\) 에서는 \(Q_{B}\) 네트워크에서 Q 값을 가져옵니다. 이렇게 두 개의 Q-network 를 같이 사용하면 Q 값이 불필요하게 커지는 것을 막을 수 있다는 것이 Double DQN 의 핵심입니다.

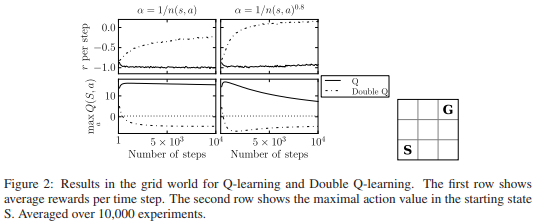그림 4. “Double Q-Learning” 에서 예로 든 Grid world 는 3x3 의 작은 크기였습니다. 우측 하단의 S 가 시작점, G 가 목표점입니다.

그런데 위에서 살펴본 것처럼 DQN 에는 이미 target network 라는 아이디어가 적용되어 있었습니다. 이 논문을 쓴 Hado van Hasselt 는 Deepmind 로 가서 2016년에 DQN 에 Double Q-Learning 을 적용하는 논문인 “Deep Reinforcement Learning with Double Q-learning” 을 David Silver 와 함께 발표했습니다.

\[Q(s, a;\theta) \rightarrow R + \gamma max Q(s', a';\theta^{-})\]

위 식은 아래처럼 바뀝니다.

\[Q(s, a;\theta) \rightarrow R + \gamma max Q(s', argmaxQ(s',a';\theta);\theta^{-})\]

행동을 선택하는 부분에 기존 Q-network 를 사용하고, 선택된 행동으로 target network 에서 Q 값을 가져옵니다. 수식이 너무 많아서 보시기에 힘드실 수도 있을 것 같습니다. 위에서 본 것처럼 학습 구조도로 나타내면 아래와 같습니다.

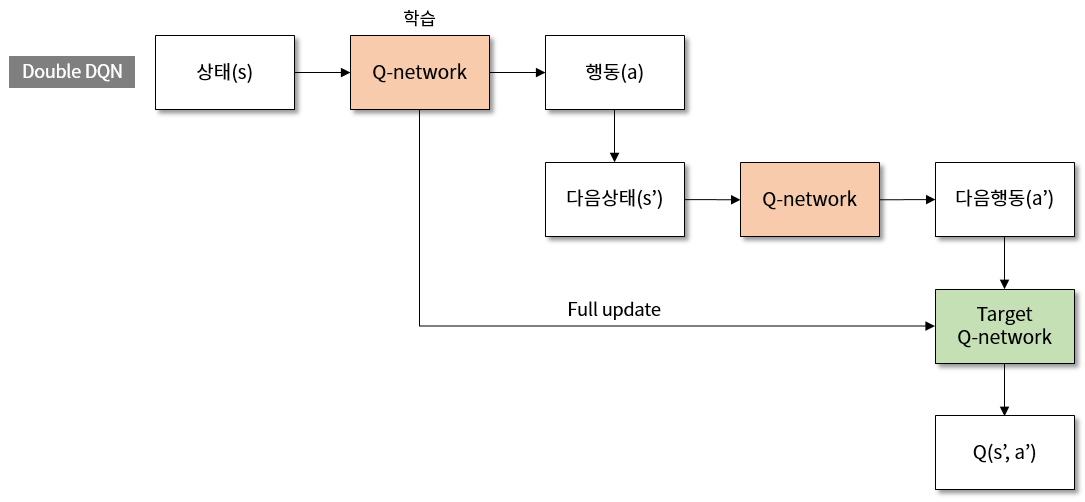그림 5. Double DQN 의 학습 구조도

인터랙티브 예제와 함께 Double DQN 이 적용된 결과를 확인해보겠습니다.

Double DQN 과 뒤에서 설명드릴 Dueling DQN 에는 soft update + learn step 10->1 + glorot initialization 도 적용되어 있습니다. 강화학습은 실행에 따라 결과값이 달라질 수 있기 때문에, Random, DQN, DQN-softupdate, Double DQN 의 퍼포먼스를 그래프로 정리해 보았습니다.

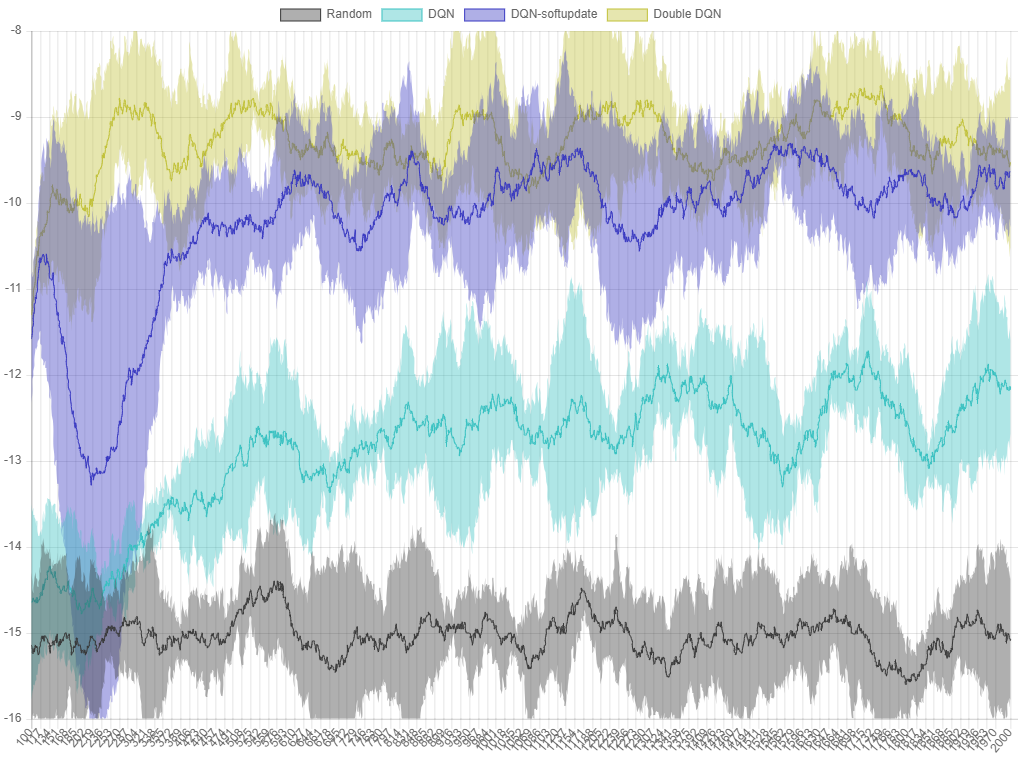그림 6. ball-find-3 에서 각 알고리즘의 퍼포먼스 그래프. X 축은 episode, Y 축은 최근 100 번의 시행에서 얻은 reward 의 평균입니다.

각 알고리즘은 5회 실행 후 평균 값을 선으로, 최대값과 최소값을 영역으로 표시했습니다. Double DQN 을 적용한 버전이 DQN-softupdate 보다 좋은 퍼포먼스를 보이는 것을 확인할 수 있습니다.

Dueling DQN

Dueling DQN 은 Q 값을 구하기 전에 네트워크의 결과값을 V 와 A 로 나눈 다음에 다시 합치겠다는 아이디어입니다. V 는 이 시리즈의 첫번째 글에서 보았던 가치 함수에 해당하는 값이고, A 는 Advantage 라는 값입니다. A 는 각 행동별로 계산되는 값이기 때문에 Q 값과 비슷하다고 생각하면 편합니다. 여기서 중요한 점은 V 를 계산할 수 있다는 것입니다. 각 상태에 대한 V 를 계산해서 Q 에 아래와 같이 더해줍니다.

\[Q(s, a) = V(s) + A(s, a) - \frac{1}{|A|}\sum_{a} A(s, a)\]

Q 값을 구할 때 V 값이 일괄로 더해지기 때문에 높은 V 값을 가진 상태의 Q 값은 결과적으로 올라갈 것이고, 반대의 경우는 Q 값이 낮아질 것입니다. 따라서 에이전트는 높은 Q 값(높은 V)이 이끄는 상태로 이동하게 되고, 낮은 Q 값(낮은 V)을 주는 행동은 피하게 됩니다. 이렇게 가치와 행동에 대한 정보를 분리해서 갖게 되는 아이디어는 다음 시간에 소개해 드릴 Actor-Critic 알고리즘에도 비슷하게 적용되었습니다.

위의 Double DQN 과 다르게 Dueling DQN 은 네트워크 구조가 바뀝니다. 마지막에 행동을 선택하는 output layer 로 합쳐지는 것은 동일하지만, 중간에 V 와 A 를 따로 계산했다가 합쳐서 최종적으로 Q 값을 계산해서 행동을 선택하게 됩니다.

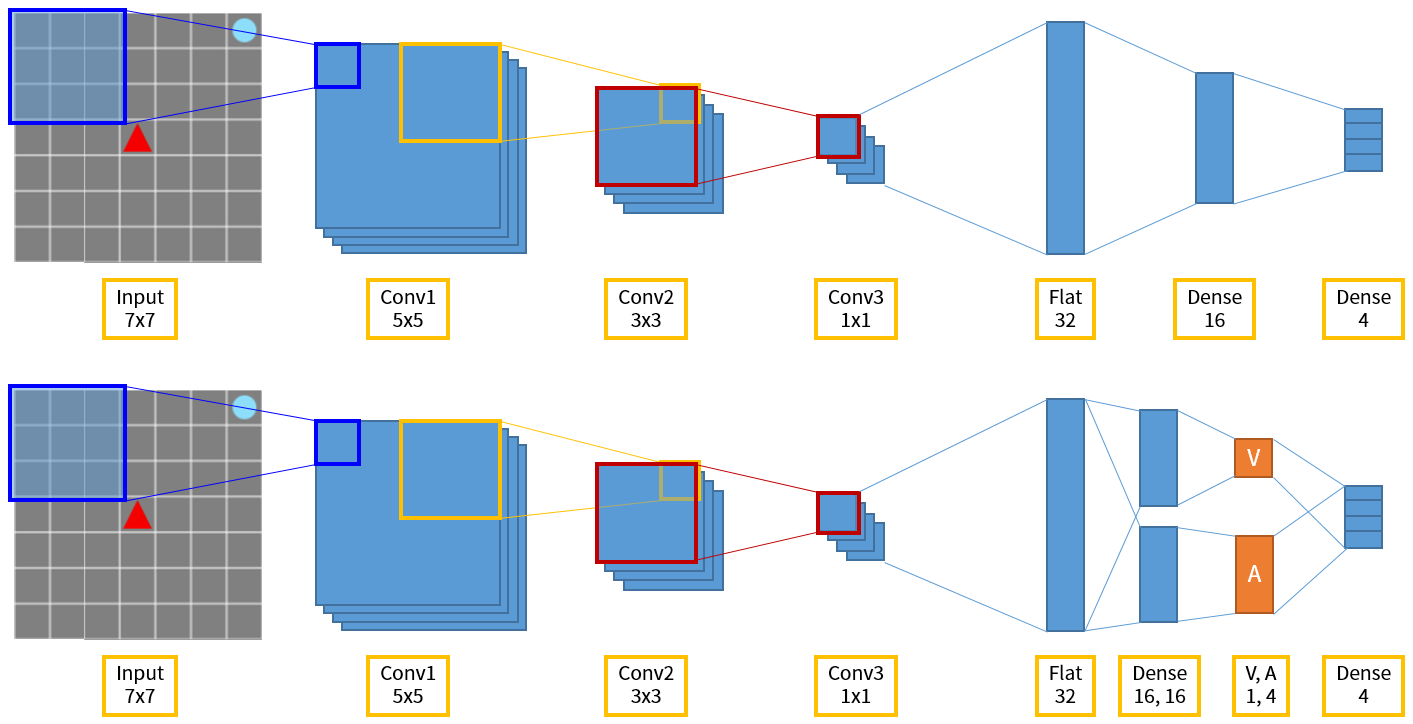그림 7. 위는 Grid World 에서의 DQN 네트워크 구조, 아래는 Dueling DQN 입니다.

Dueling DQN 의 퍼포먼스 역시 기존 soft update 버전보다 좋아집니다. Double DQN 과 Dueling DQN 을 같이 적용한 버전을 DDDQN(Dueling Double Deep Q-Network) 이라고 부르기도 합니다.

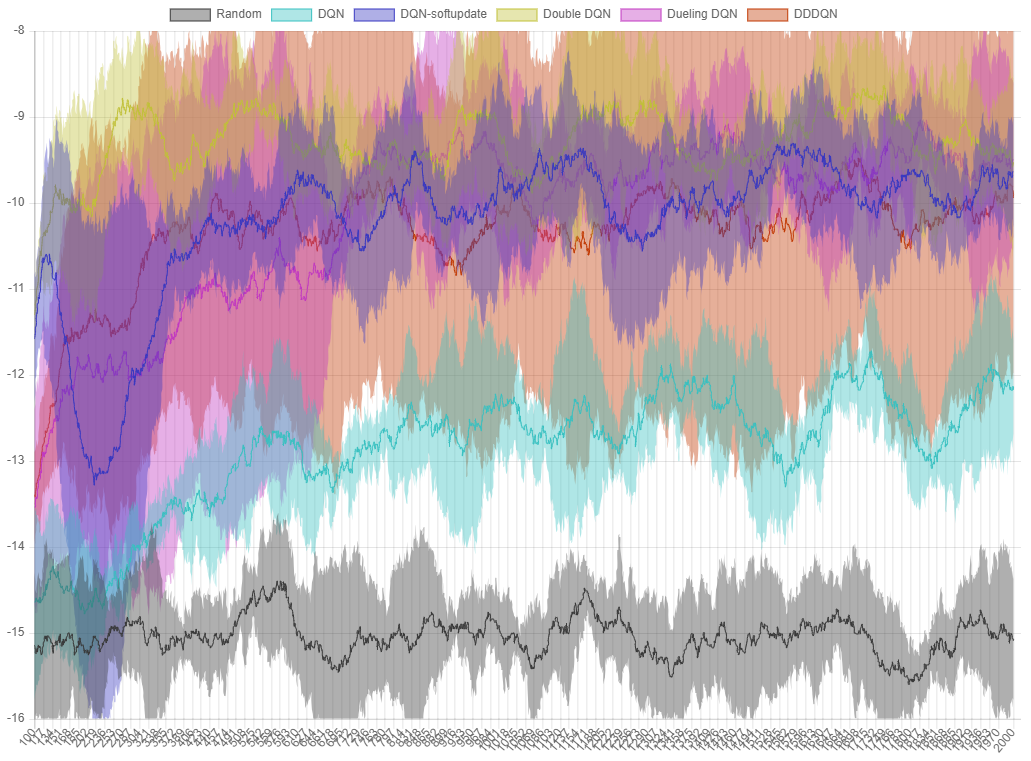그림 8. ball-find-3 에서 각 알고리즘의 퍼포먼스 그래프. X 축은 episode, Y 축은 최근 100 번의 시행에서 얻은 reward 의 평균입니다.

Dueling DQN 은 DQN 보다는 좋은 퍼포먼스를 보이고, soft update 버전과는 비슷한 퍼포먼스를 보입니다. Dueling 과 Double 을 합친 DDDQN 도 이 문제에서는 그다지 좋은 퍼포먼스를 기록하지 못했지만 파라미터 튜닝 등을 통해 결과값을 개선할 수 있을 것으로 보입니다.

 

Deep SARSA

어떤 문제는 복잡한 알고리즘보다 간단한 알고리즘이 더 효과적일 수도 있습니다. 이 Grid World 에서 ball-find-3 문제의 경우, Deep SARSA 알고리즘이 DQN 보다 더 좋은 퍼포먼스를 보였습니다. SARSA 는 우리가 위에서 계속 봐왔던 상태(s), 행동(a), 보상(r), 다음 상태(s’), 다음 행동(a’) 을 합친 말입니다.

Q-learning 을 SARSA 와 비교하면 상태(s), 행동(a), 보상(r), 다음 상태(s’) 까지만 사용하는 SARS 라고 말할 수 있겠습니다. 따라서 Q-learning 과 SARSA 의 차이는 다음 행동(a’) 이 학습에 필요한지 여부가 됩니다.

\[Q-learning : Q(s, a) = Q(s, a) + \alpha (R + \gamma max Q(s', a') - Q(s, a))\] \[SARSA : Q(s, a) = Q(s, a) + \alpha (R + \gamma Q(s', a') - Q(s, a))\]

SARSA 의 식에는 max 연산자가 빠진 대신 \(Q(s', a')\) 가 들어가 있습니다. Q-learning 이 다음 스텝의 max-Q 값을 구하는 greedy 한 방법이라면, SARSA 는 에이전트가 다음 스텝에서 취한 행동의 값을 직접 사용하는 stochastic 한 방법이라고 할 수 있습니다. Q-learning 은 max 값을 구해야 하기 때문에 episode 의 실행이 끝난 다음에 수행해야 하는 Off-policy 알고리즘이지만, SARSA 는 episode 의 실행 중에 언제든지 학습이 가능한 On-policy 알고리즘이라는 특성도 있습니다.

Deep SARSA 는 DQN 과 마찬가지로 Q 값을 구하는 Q-network 로 딥러닝 신경망을 적용한 것입니다. 그럼 이 문제에서 Deep SARSA 가 얼마나 좋은 성능을 보이는지 인터랙티브 예제에서 확인해보겠습니다.

DeepSARSA 에이전트는 -8~-10 정도의 avg. reward 를 얻게 됩니다. 학습이 종료된 뒤 RUN(DeepSARSA) 버튼을 눌러보면 DQN 보다 에이전트의 움직임이 더 효율적인 것을 확인할 수 있습니다.

여기까지 DQN 을 개선할 수 있는 몇 가지 방법들과, DQN 과 비슷하지만 On-policy 방법인 DeepSARSA 에 대해서 살펴보았습니다. 다음 시간에는 Dueling DQN 과 비슷한 개념을 가지고 있는 Actor-Critic 에 대해서 알아보고 새로운 문제도 풀어보도록 하겠습니다. 추가로 Actor-Critic 알고리즘으로 ball-find-3 문제를 2,000 episode 동안 훈련시킨 에이전트의 움직임을 첨부해봅니다. 이 알고리즘에 대해서는 다음 시간에 분석해보도록 하겠습니다.

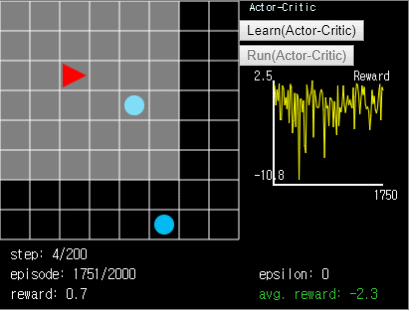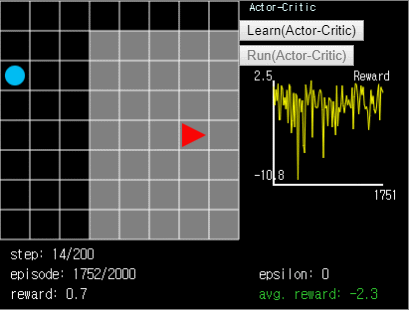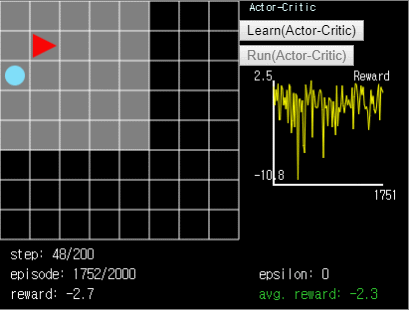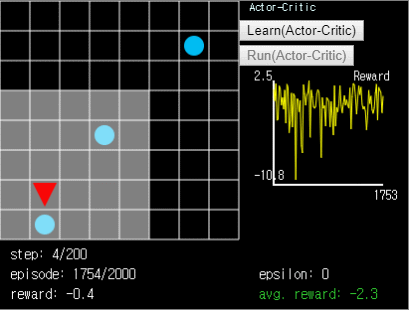그림 9. Actor-Critic 에이전트. ball-find-3 에서 avg. reward 는 -2.5~-1.5 정도가 나옵니다.

그리고 지금까지 살펴본 알고리즘들의 퍼포먼스를 정리해 보았습니다. 인터랙티브 그래프이기 때문에 상단의 항목을 on/off 하며 보고 싶은 항목만 비교해볼 수 있습니다.

지난 글보다 수식이 훨씬 많아져서 보시기에 부담스러우셨을 수도 있을 것 같습니다. 쉽지 않은 내용이지만 다음에도 최대한 쉽게 풀어낼 수 있도록 노력하겠습니다. 긴 글을 끝까지 읽어주셔서 감사합니다.