Shadertoy 메타볼 분석
12 Dec 2018 • 0 Comments
도입
지난 글에 이어, 이번에는 3D 그래픽스의 가장 기본적인 구현 요소 중 하나인 메타볼에 대해서 알아보겠습니다. 이번 포스팅의 아이디어는 Ryan Geiss 라는 분이 쓴 이 글에 많이 의존하고 있다는 점을 미리 밝혀드립니다. 홈페이지를 보니 이 분은 2010년부터 Google 에서 일하고 있네요.
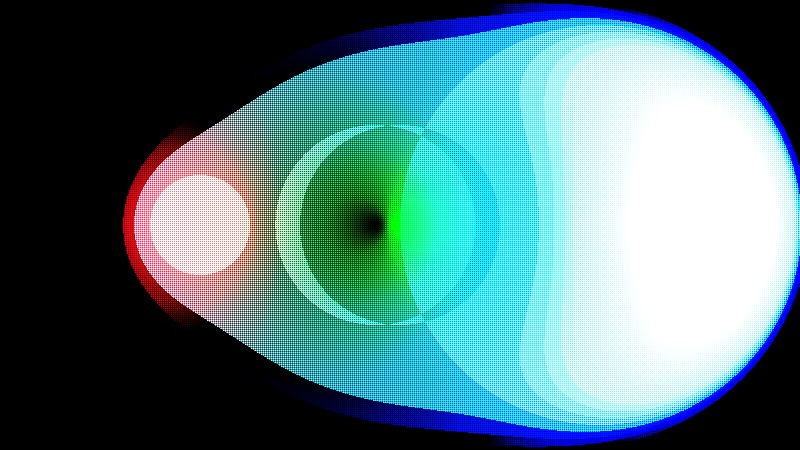
오늘 분석할 Shadertoy 의 코드는 많은 메타볼 구현체 중 어렵게 고른 Metaballs - kinda yellow입니다. 단순하면서도 비주얼적으로 아름답게 보이는 것을 찾기 위해 노력했습니다. 그럼 시작해보겠습니다.
좌표 관련 기본 코드
본격적인 내용에 앞서서 여기에도 좌표 관련 기본 코드가 추가로 나오고 있어서 짚고 넘어가도록 하겠습니다.
지난 글에서 vec2 uv = fragCoord/iResolution.xy; 가 스크린의 크기 변화에 관계없이 각 픽셀에 대응하는 uv.x, uv.y 값을 각각 0.0~1.0 사이의 값으로 제한해주는 것이라고 정리했습니다. 이 코드는 shadertoy 에서 가장 많이 쓰이는 boilerplate code 라는 설명도 같이 했습니다.
그런데 shadertoy 코드의 11행과 15행에도 기본 좌표를 변경하는 코드가 있습니다.
11행 : uv -= .5;
15행 : uv.x *= iResolution.x / iResolution.y;
먼저 11행에 대해서 알아보기 위해 코드를 넣어보겠습니다.
5행의 주석에 uv -= .5; 가 추가되어 있습니다. 주석을 해제하면 화면이 전반적으로 어두워지는 것을 확인할 수 있습니다. 화면 전반적으로 0.0~1.0 범위에 있던 uv.x, uv.y 값에서 0.5 를 뺐기 때문에, 그 범위는 -0.5~0.5 가 된다는 것을 짐작할 수 있습니다.
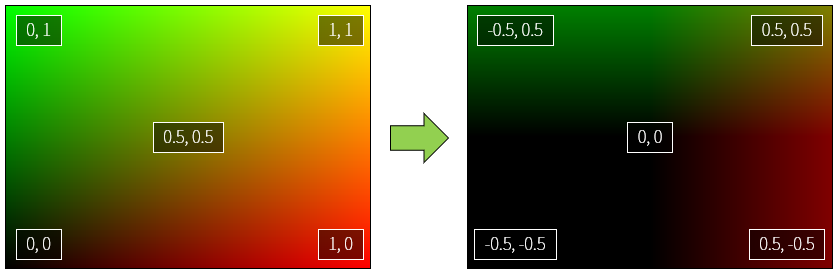
shader 의 컬러 값은 0.0~1.0 만 유효한 값으로 인정하고, 나머지는 clip 됩니다. 즉 음수는 0.0 으로, 1.0 을 초과하는 양수는 1.0 으로 계산됩니다. 따라서 음수가 많아졌기 때문에 화면에 검은색의 비율이 높아지고 전반적으로 어두워진 것입니다.
화면 중앙의 좌표가 (0.5, 0.5) 에서 (0, 0) 이 된 것을 주목해주십시오. 이렇게 되면 화면 중앙을 중심으로 원 등의 도형을 그리기가 수월해집니다. 중학교 1학년 때부터 배우는 좌표평면을 생각하시면 이해가 쉬울 것 같습니다.
그럼 15행의 uv.x *= iResolution.x / iResolution.y;은 무엇일까요?
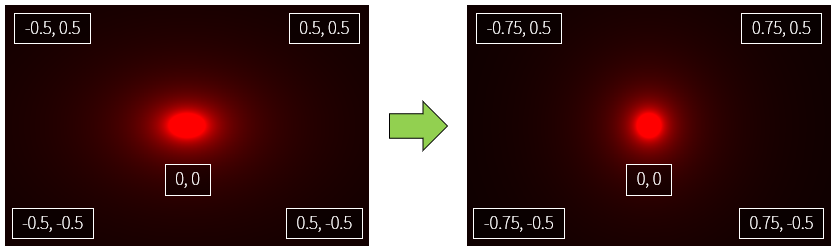
일단 circle 함수가 추가되었는데 이 부분은 바로 뒤에 설명드리도록 하겠습니다. 먼저 10행의 주석을 해제하며 차이를 직접 확인해보시기 바랍니다. 원의 너비가 달라지는 것이 느껴지시나요?
uv.x *= resolution.x / resolution.y; 를 뜯어보면 이 식은 uv.x 에 (screen 의 x 크기 / screen 의 y 크기)를 곱해줍니다. 보통 모니터는 가로가 세로보다 넓은 스크린이 많기 때문에, 가로/세로를 같은 비율로 표현한다면 원래 예제의 원처럼 찌그러진 상태로 표현될 것입니다. 이 식은 그에 대해 비율을 정규화시켜서 가로/세로 비율이 1:1 로 보이도록 하는 효과를 갖습니다.
그럼 이제 circle 함수에 대한 이야기를 할 때가 온 것 같습니다.
Circle 함수
Circle 이라고 하면 아무래도 중학교때 배우는 원의 방정식을 기억하시는 분이 많으실 것 같습니다.
\[x^2+y^2=r^2\]이 식을 shader 로 표현하면 이렇게 볼 수 있습니다.
circle 함수를 먼저 뜯어보면, circle 함수의 인수는 uv 하나입니다. 그리고 distance 는 shader 에서 쓰는 내장 함수 입니다. 이름 그대로 벡터와 벡터 사이의 거리를 구할 수 있습니다. 자세한 내용은 The book of shaders 의 distance에 예제와 함께 설명이 되어 있습니다.
스크린의 중심이 (0., 0.) 이기 때문에 이 점과 모든 점의 거리를 구하면 자연스럽게 원의 영역이 만들어집니다. 원의 정의는 한 점에서 거리가 같은 모든 점의 집합이기 때문입니다.
여기서는 거리 정보를 gl_FragColor 의 R 채널에 넣었습니다. 그 결과 거리가 멀어질수록 빨간색이 진해집니다. 원의 영역을 뚜렷하게 구분하고 싶으면 step function 을 사용합니다. 이 함수는 두번째 인수가 첫번째 인수보다 작으면 0.0 을, 그렇지 않으면 1.0 을 반환합니다. The book of shaders 의 step 페이지에서는 첫번째 인수를 edge 라고 명명하고 있습니다.
step 함수를 쓴 결과를 알아보기 위해 5행의 주석을 해제합니다. 경계선이 뚜렷한 원이 생긴 것을 보실 수 있습니다. 0.2 보다 작은 값은 모두 0.0 이 되고, 그렇지 않으면 모두 1.0 이 되기 때문입니다.
눈치채신 분도 있겠지만 vec(0., 0.)은 원의 중심 역할을 합니다. 즉 이 값을 바꾸면 원의 중심이 바뀌어서 평행이동을 시킬 수 있습니다. 이것을 따로 pos 라는 인수로 빼서 사용한 것이 이 글의 두번째 예제에 나왔던 circle 함수입니다.
그런데 우리는 보통 원을 그릴 때 바깥쪽 영역보다 안쪽 영역이 궁금한 경우가 많습니다. 즉 안쪽을 색칠해서 원으로 쓰고, 나머지 빈 공간은 무시하는 경우를 말합니다. 이렇게 하기 위해서는 어떻게 해야 할까요? 앞의 원의 방정식에서 \(x^2+y^2\) 로 양변을 각각 나누면 아래와 같은 식이 됩니다.
\[1 = \frac{r^2}{x^2+y^2}\]이 등식의 양변에 루트를 취하면 오른쪽 항의 분모는 \(\sqrt{x^2+y^2}\) 가 됩니다. 이 식은 원점 (0,0) 에서 (x,y) 까지의 거리를 나타내는 값이 됩니다. shader 에서는 내장 함수인 distance 로 축약해서 쓸 수 있습니다. 그리고 원점 (0,0) 의 자리에 pos 인수를 넣으면 두번째 예제에서 보셨던 circle 함수가 됩니다. 오른쪽 항의 분자에 해당하는 부분은 루트를 취했기 때문에 \(r^2\) 에서 \(r\), 즉 원의 반지름이 됩니다. 두번째 예제에서는 0.05 를 사용했습니다.
float circle(vec2 uv, vec2 pos) {
return 0.05/distance(uv, pos);
}
아래 코드에서는 G 채널에도 값이 들어가서, 원래 shadertoy code 인 Metaballs - kinda yellow와 같은 색조합을 볼 수 있습니다.
단순히 step 함수로 영역을 표시해주는 것보다 미적으로 더 괜찮아 보입니다. 색깔 지정을 바꿔가며 테스트해보시면 더 멋진 결과를 찾으실 수도 있을 것 같습니다.
11행을 주석처리하고 12행의 주석을 해제하면 원의 중심이 이동하는 단순한 애니메이션을 볼 수 있습니다. 첫 시간에 time 변수를 이용해서 색깔이 변하게 했던 것을 기억하시나요? 원의 중심에 time 변수를 넣으면 시간에 따라 중심 좌표가 바뀌기 때문에 중심이 이동합니다. 보통 x=cos(time), y=sin(time) 으로 넣지만 원본 코드처럼 반대여도 상관없습니다.
그럼 이제 다음 부분으로 넘어가도록 하겠습니다. 절반 이상 왔네요.
여러 개의 도형 더하기
한 개의 원을 그렸는데, 2개 이상의 원은 어떻게 표현해야 할까요? shader 에서는 엄청나게 쉽습니다. 바로 색깔을 더해주면 됩니다.
원래 코드에서는 먼저 circle 함수로 c 라는 float 변수에 원을 하나 정의한 다음, 다른 circle 을 c 에 더해줬습니다.
float c = circle(uv, vec2(sin(time * 2.) * .4, cos(time * .4) * .4), r);
c += circle(uv, vec2(sin(time * .5) * .4, cos(time * .7) * .4), r);
c += circle(uv, vec2(sin(time * .7) * .4, cos(time * .8) * .4), r);
...
결과는 우리가 확인할 수 있는 것처럼 여러 개의 원이 더해진 결과였습니다. 실제로 그렇게 되는지 한번 해보겠습니다.
결과는 잘 나옵니다. 그런데 잠깐만요. 가운데 원이 조금 커보이지 않습니까? 착시일까요? 결과를 확인하기 위해서, 각 원의 좌표를 좀 더 가깝게 해보면 어떨까요? 결과는 아래와 같습니다.

위쪽 원은 아래쪽보다 거리를 좀 더 가깝게 배치한 것입니다. 확실히 가깝게 붙을수록 원이 점점 커집니다.
이것은 이 코드의 circle, 나아가서는 메타볼 공식이 단순한 원이 아니라 주변에 대한 영향력(influence)을 나타내고 있기 때문입니다.
메타볼
포스팅 첫부분에서 언급했던 Ryan Geiss 는 메타볼에 대해서 이렇게 쓰고 있습니다.
The function [f(x,y,z) = 1.0 / (x^2 + y^2 + z^2)] might look familiar to people who’ve studied physics. This is the equation for the strength of the electric field due to a point charge at the origin. … The electric field is infinity at exactly the point where the charge lies, and drops off quickly as you go away from the charge. But no matter how far away you are from that point, it still has some contribution.
볼드체로 강조한 부분과 주변을 번역해보자면, 메타볼 공식은 한 점 주변의 전기장의 힘과 같다고 볼 수 있고, 메타볼(원)과 가까운 부분은 당연히 그 힘의 영향력이 아주 강하겠지만 중심에서 멀리 떨어진 점도 일정 부분의 영향력을 가진다는 말입니다.
영향력이 합쳐진다는 것을 Ryan Geiss 의 글에서는 band 를 나눠서 알아보기 쉽게 표현하고 있습니다. 우리도 해볼 수 있습니다.
6행의 return floor(r/distance(uv, pos) * 5.) / 5.; 에서는 floor 함수를 썼습니다. floor 는 계단 함수로, 실수에서 소수점을 날리는 역할을 합니다. python 의 int(), javascript 의 Math.floor() 와 같은 역할입니다.
이 함수를 거치면 메타볼이 1차적으로 만드는 모든 값은 0, 0.2, 0.4, 0.6, 0.8, 1.0 중 하나가 됩니다. 메타볼들이 겹칠 때는 이 값들이 서로 합쳐지면서 바뀌는 것을 확인할 수 있습니다. 특히 겹쳐질 때 노란색 원의 크기가 커지는 것을 볼 수 있습니다. 이것은 합쳐지는 값이 1.0 이상이 되는 영역이 늘어나기 때문입니다.
나머지 부분도 기존 코드에서 옮겨야 할 부분들을 모두 옮겼습니다. 5행의 주석을 해제하면 원본과 같은 모습이 됩니다. 원본과 비교하면서 three.js 에서는 어떤 부분이 달라지는지 알아보는 것도 재미있을 것 같습니다.
이것으로 두번째 shadertoy 코드 분석글을 마칩니다. 다음 시간에는 조금 더 재미있는 코드와 함께 돌아오겠습니다. 긴 글 읽어주셔서 감사합니다.