Creating a Queens game map on Linkedin

13 May 2024 • 0 Comments

• Intro
• N-queen Problem
• Diagonal placement condition for the Queens problem
• The area condition in the Queens problem
• Outro

image link

 

Intro

LinkedIn is a recruitment and job search site with over 1 billion members worldwide, and its weekly active users (WAU) reach 65 million.¹ Although it is a social networking service, unlike Instagram or TikTok, it is a place where serious discussions about careers and work are prevalent. However, recently (as of May 1, 2024), three games were added to LinkedIn, which caused controversy as it didn’t seem to fit the atmosphere of the platform.

However, if we think about it, adding casually playable games is something that social networking sites like Facebook have been doing since ancient times, and even The New York Times has various games, including crossword puzzles. The acquisition of Wordle, which gained tremendous popularity after its launch in 2021, by The New York Times at a high price was a very famous event in the industry.²

It seems that LinkedIn also recognized the importance of adding casually playable games, as the three games added this time all take only 5 to 10 minutes to play. Among them, two of the games are language-related, so algorithmically generating them seems not so simple (although it could be done quickly using LLM, we won’t delve into it here). Instead, in this blog, we will discuss how to generate maps for a game called Queens.

 

N-queen Problem

To understand the Queens game, you first need to know the N-queen problem. The N-queen problem, where N queens must be placed on an NxN board in positions where they do not attack each other, can be very time-consuming to solve indiscriminately, but it is a well-known algorithm problem that can be relatively easily solved by modifying the conditions for solving the problem.

Example solution for the 4-queen problem

In chess, queens can move to any square on the same row, same column, or diagonal from their current position. Therefore, to avoid attacking each other, the queens must be placed so that they do not overlap in rows, columns, or diagonals.

To simplify the problem slightly, let’s consider rooks instead of queens. Rooks can move only along rows and columns, not diagonally.

Example solution for the 4-rook problem: The rooks are placed in rows & columns 0, 1, 2, and 3 respectively.

A common feature seen in the solutions for both N-queen and N-rook problems is that neither queens nor rooks can be placed more than once in the same row or column. When placing rooks one per row sequentially, as long as each rook is in a different column, it constitutes a solution to the N-rook problem.

Code 1. Code for finding the solution to the N-rook problem

 

The search(arr) function in the above code starts with an empty array and proceeds to find the column numbers of the rooks to be placed on each row. The termination condition of the search(arr) function, as seen in line 19, is when the length of arr is equal to N. Otherwise, if there is a number i from 0 to N-1 that is not already in the current arr, it finds it and calls a new search([...arr, i]) function. While not all results are displayed in the result pane on the right due to space constraints, you can verify that the number of solutions for N=4 is 24. By changing the N in line 30 to 5, 6, 8, and so on, you’ll notice that this number corresponds to the factorial function learned in mathematics. Hence, the number of solutions to the N-rook problem is \(N!\).

So, how would you solve the N-queen problem? You can slightly modify the search function in the above code to check for diagonal conditions. It involves checking if there are any queens already placed in diagonal positions with the new number i being added to the arr. Below is the code representation of this modification.

Code 2. Code for finding the solution to the N-queen problem.

  The additional condition added after the if statement on line 24 is arr.filter((c,idx) => Math.abs(i-c) == Math.abs(arr.length-idx)).length == 0. This checks if there are no elements in the current arr where the difference in columns (Math.abs(i-c)) and the difference in rows (Math.abs(arr.length-idx)) for the queen to be placed in the arr.length-th row and the i-th column are equal. If there are no such elements, it means that the placement is possible, so the search([...arr, i]) function with i added to arr is called. The number of solutions reduces to 2 when N=4. Changing N to 8 in line 30 reveals that the answer is 92. The number of solutions has decreased significantly compared to the N-rook problem.

The arrangement of queens on the first solution for N=8, placed in the 0th, 4th, 7th, 5th, 2nd, 6th, 1st, and 3rd columns.

 

Diagonal placement condition for the Queens problem

However, the diagonal placement condition in the Queens problem is slightly different from the N-queen problem. While the condition remains that only one queen should be placed in each row and column, in terms of diagonals, two queens can be adjacent to each other as long as they are not in the same diagonal. In other words, as long as they are one square apart diagonally, it is acceptable.

Code 3. Code for finding the solution to queen placement in the Queens game.

The condition in the if statement on line 24 has changed from checking the entire queens in arr to checking only the last queen (arr[arr.length-1]). Since queens are placed sequentially in each row, for example, if placing a queen in the 3rd row, there’s no need to consider the queen in the 1st row, only the queen in the 2nd row needs to be considered. With this change, the number of solutions for N=8 becomes 5,242. This is an increased quantity compared to the original N-queen problem.

The arrangement of queens on the first solution for N=8, placed in the 0th, 2nd, 4th, 1st, 5th, 7th, 3rd, and 6th columns.

 

The area condition in the Queens problem

However, the Queens problem goes one step further. In addition to the conditions mentioned earlier, each queen must be placed only one per area of the same color. For example, the arrangement of queens in the columns 02415736, as examined above, can be represented with the added area condition as follows:

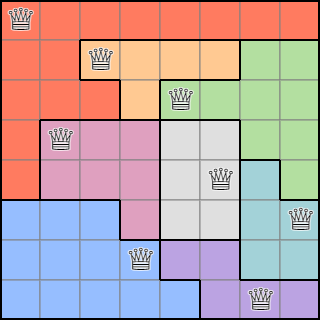8x8 체스판을 8개의 영역으로 나누고 각 영역에 1개의 퀸만 배치되도록 한 모습

An arrangement where an 8x8 chessboard is divided into 8 regions and only one queen is placed in each region. In this case, the regions must be connected to each other, each cell belongs to only one region, and all cells must belong to exactly one region, which seems to be implicitly applied. This scenario corresponds to the N=8 case in the Linkedin Queens game, and by using one of the 5,242 queen placements obtained earlier and randomly assigning regions, we can obtain a map that looks similar to the one offered in the Linkedin Queens game. However, whether it will be fun or not is a different issue, and this blog will not delve into that aspect.

To satisfy the region condition, we start with the queen placement state from Code 3. First, we designate each cell where a queen is placed as a different region.

The depiction of the cells on the chessboard designated as different regions where queens are placed.

Next, we designate as candidates the neighboring cells, vertically and horizontally, that have not yet been assigned a region.

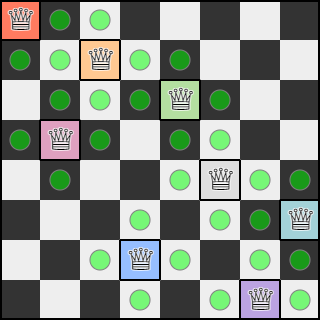Visualization of the designated candidates.

Next, we randomly select one of these candidates and assign it to one of its adjacent regions. Then, we update the list of candidates.

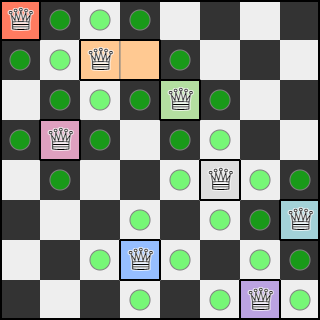After designating the candidate at row 1, column 3 to a region, update the list of candidates.

By repeating this process, we can obtain a random region condition map based on the queen placements.

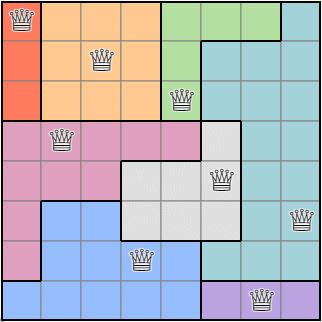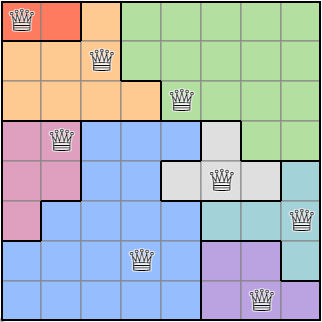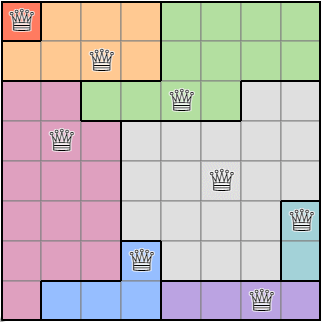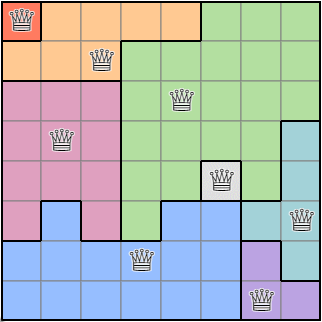Execution result of the algorithm for obtaining the region condition.

 

Outro

In this post, we explored how to create maps for the Queens game added to LinkedIn. We also have various articles in mind about generating game levels using PCG, so we appreciate your interest. Feel free to inquire about any further questions you may have. Thank you for reading this lengthy post.