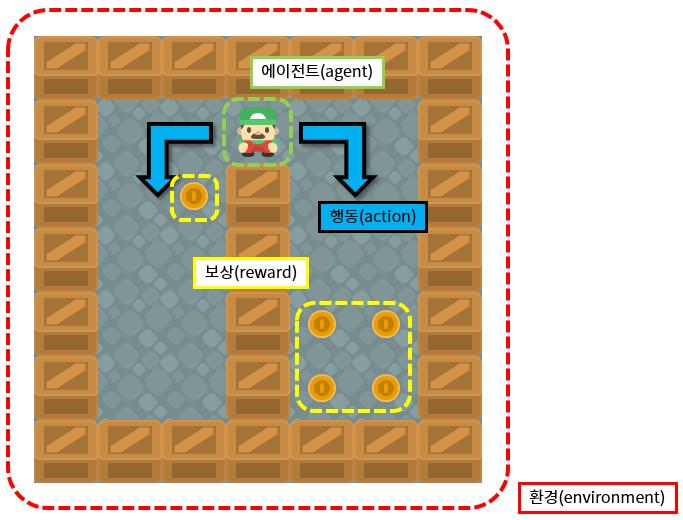
Learn Reinforcement Learning (1) - Value Function

10 Feb 2019 • 0 Comments Tags:

[ reinforcement-learning ]

What is reinforcement learning?
Theoretical background
Grid World
Value Function

What is reinforcement learning?

In 2016, AlphaGo versus Lee Sedol became the topic of the event in which artificial intelligence won the world’s first professional supremacy in Baduk. In 2018, OpenAI’s researchers at DOTA2, a 5-to-5 team-fighting game, won a pro-amateur team in a pre-determined heroic confrontation, and in 2019 Deepmind’s AlphaStar won the best professional player in StarCraft 2(Protoss versus Protoss).

Reinforcement learning is an algorithm that learns the current state of an agent in a given environment and learns in the direction of maximizing reward through action. Actions that increase rewards are more frequent, and less rewarding actions.

In this process, reinforcement learning makes mistakes through multiple attempts, gradually corrects the mistakes, and gradually finds the answers that you want. It can be said that it is a way to simplify and to say to try once and fix it gradually.

Sokoban Tileset by Kenney

Theoretical background

Reinforcement learning has been greatly influenced by the way humans and animals learn.

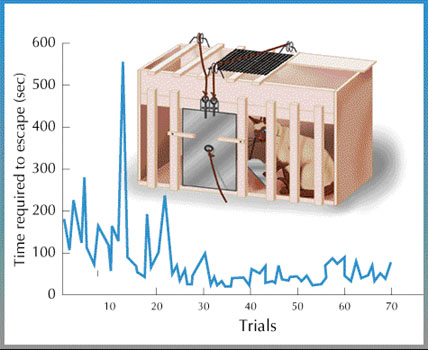
In the early 20th century, American psychologist Edward Thorndike insisted on the Law of effect through experiments with cats. When he put the cat in the box, put the fish outside, and only had to touch the lever to get out of the box, as the number of times of confinement was repeated, the cat quickly touched the lever and quickly exited the box. The law of effect is that the action - lever touch - which gives the content - fish - is reinforce.

Source link

Demis Hassabis, founder of Deepmind, received a Ph.D. in Cognitive Neuroscience from UCL, UK. Cognitive neuroscience is a study of memory and decision-making that occurs in the human brain, and is a discipline for understanding human behavior. In a special article on Nature’s 100th anniversary of Allan Turing’s birth in 2012, he said we must understand the principles of human brain’s behavior, which were considered black boxes and did not need to know the principles of operation, to the level of algorithms to create more advanced artificial intelligence.

Richard Sutton and Andrew Barto, pioneers of reinforcement learning, described the Temporal difference model, an effective model from the beginning of reinforcement learning, through animal learning theory. The time difference learning model is the most important reinforcement learning concept together with the Monte Carlo model. We will discuss these two things in the next article.

Grid World

Artificial intelligence, including reinforcement learning, has long been a problem in Grid World, which has simplified the real world. Grid World can place agents, goals, rewards, etc. on a grid with limited space in two dimensions and solve problems with various algorithms.

let canvas = document.getElementById('editor_canvas_0');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Step(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];

button.onclick = function() {
    if (is_running) return;
    iterate(false);
}

button2.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let action = Math.floor(Math.random() * 4);
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 60);
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

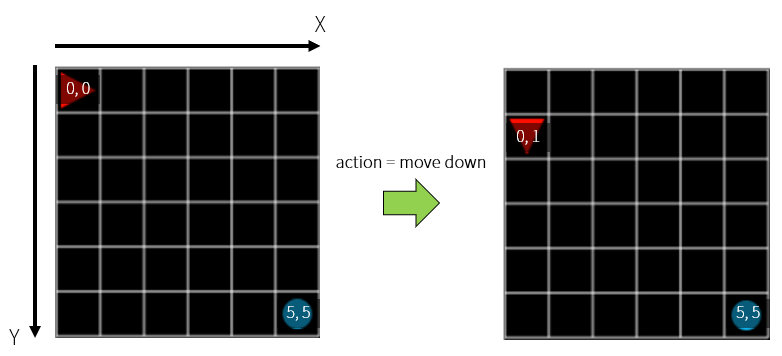
Here is a simple example of Grid World.¹ A red triangle(🔺) represents the agent, and a blue circle(🔵) represents the goal that the agent should reach.

Here, when the agent reaches the same grid as the target within a given time step, it succeeds, one episode ends, and the next episode begins. To reach the target, the agent can perform an action that moves to one of the four grids(up, down, left, and right) that touch the current position at each step. At the end of the grid, movement is restricted(no movement to the grid-free location).

When the agent reaches the target, he receives +1 reward and receives a reward (penalty) of -0.1 every step to give an incentive to the quick reward seeking action. These settings are necessary because agents in reinforcement learning act toward maximizing compensation and less in the opposite direction.

Once the “Step(random action)” button is pressed, the agent performs a single action, and pressing the “Loop(random action)” button automatically performs an action until the total Episode reaches 100. At every step, the agent randomly selects one of the possible actions. It is not reinforcement learning yet. Agents only move randomly like molecules in the air. If the agent is lucky, he can reach his goal, but most of the time he does not, and the episode ends at a location away from the target.

In order for an agent to find a goal well, you first need to know where it is. That is, you need to know state information about the environment. Currently, Grid World is made up of 36 grids totaling 6 on one side. In the initial state, the agent is located in the first cell (x = 0, y = 0) and the target is located in the last cell (x = 5, y = 5). If we move down here, the agent’s position will be (x = 0, y = 1).

Random execution of the above steps will reward each step and combine them together to become the final reward displayed in the final graph. Let’s take one episode as an example.

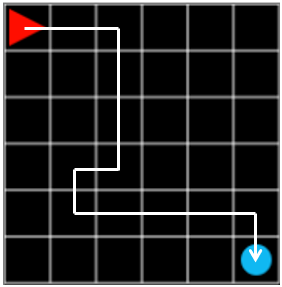Figure 1. steps: 12, reward: -0.1

In the episode of Figure 1, the agent was a little lost, but succeeded in finding the target. The final reward is \(-0.1 \times 11 + 1.0 = -0.1\) because -0.1 for each step and +1 for the target at the end.

What about saving the grids from this episode and storing the reward we received there?

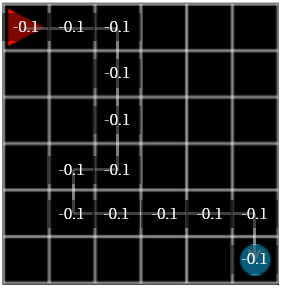Figure 2

The next action is to refer to the reward that was stored in the grid, not the random action. When choosing which grid to move, select the grid with the largest reward, and if more than one are equal, choose one of them at random. And the initial reward value is all zeros.

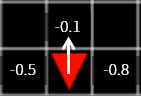Figure 3. Agent moves to the grid with the highest reward of -0.1.

It will update the value of the grid while repeating the episode. How do we update? 1) Overwrite with new value, 2) Take average. The second option appears to be more stable than the first one.

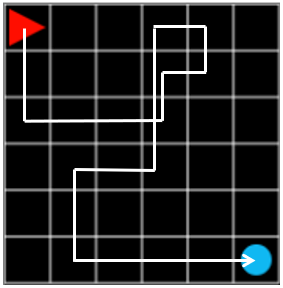Figure 4. steps: 20, reward: -0.9

In the episode shown in Figure 4, the agent wandered a bit further but succeeded in finding the target. The final reward is \(-0.1 \times 19 + 1.0 = -0.9\) because -0.1 for each step and the final target is +1.0.

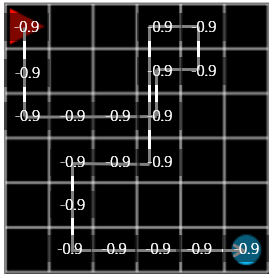Figure 5

Then, the mean of the reward values for the overlapping grids is shown in Fig. 6.

Figure 6

Then, we repeat the execution by the random action, find the reward of each grid, and act the agent according to this reward.

let canvas = document.getElementById('editor_canvas_1');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
env.maxEpisodes = 50;
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Run(by reward)';
button2.disabled = true;
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];
let value_array = new Array(env.grid_W * env.grid_W).fill(0);
let cnt_array = new Array(env.grid_W * env.grid_W).fill(0);
let stepped_array;

button.onclick = function() {
    if (is_running) return;

    is_running = true;
    stepped_array = [0];
    iterate(true);
}

button2.onclick = function() {
    iterate(true);
}

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    let max = Math.max(...value_array);
    let min = Math.min(...value_array);
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] / max * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor((1.1-Math.abs((value_array[i]-min) / (max-min+1e-4))) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function iterate(is_loop = true) {
    let action;
    if (button2.disabled) {
        action = Math.floor(Math.random() * 4);
    }
    else {
        let values = [];
        let x, y, idx;
        for (let i = 0; i < dirs.length; i += 1) {
            x = agent.x + dirs[i][0];
            y = agent.y + dirs[i][1];
            if (x >= 0 && x < env.width &&
                y >= 0 && y < env.height) {
                idx = x + y * env.grid_W;
                values.push(value_array[idx]);
            }
            else {
                values.push(-Number.MAX_VALUE);
            }
        }

        // find max values
        const m = Math.max(...values);
        values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
        action = values[Math.floor(Math.random() * values.length)];
    }
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();

    let idx = agent.x + agent.y * env.grid_W;
    if (stepped_array.indexOf(idx) === -1) {
        stepped_array.push(idx);
    }

    if (done || env.steps >= env.maxSteps) {
        let reward = Math.floor(agent.reward * 10) / 10;
        rewards_array.push(reward);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 60);
        }

        if (button2.disabled) {
            for (let i = 0; i < stepped_array.length; i += 1) {
                const idx = stepped_array[i];
                cnt_array[idx] += 1;
                value_array[idx] += (reward - value_array[idx]) / cnt_array[idx];
                value_array[idx] = Math.floor(value_array[idx] * 10) / 10;
            }

            stepped_array = [];
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
    else {
        if (button2.disabled) {
            button2.disabled = false;
            button.disabled = true;
            env.episodes = 0;
        }
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

Press the Loop (random action) button to cycle through 50 episodes, then press the Run (by reward) button to observe the agent acting according to the reward. But the agent does not find the goal well. Sometimes an agent falls into the wrong goal and ends up wandering the same place.

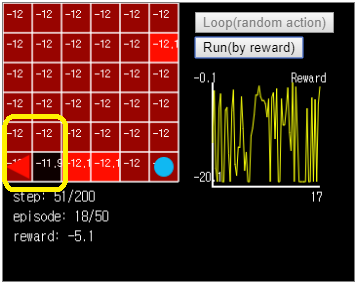Figure 7. In this case, the agent will not exit from the bottom left corner of Grid World.

One of the causes of the problem is that the reward values of each grid are almost constant. Agents that move with random actions go through too many grids before reaching the goal. So, can we distinguish between usable movements, that is, movements that contribute more to reaching the goal?

Let’s think about the problem backwards. When an agent is located just before reaching the goal (x = 4, y = 5), where should the agent move A, B, or C? Of course, moving to C would be the best choice. If you move to C, the compensation is +1, if you move to A or B, the compensation is -0.1.

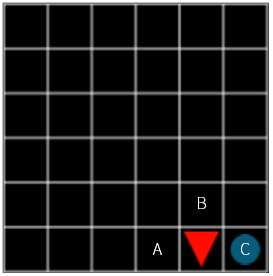Figure 8

At this point, the value of C must be higher than A and B. So, what about one location away from here? Here again, C is probably the best choice. The rewards you receive in the next step immediately are the same for both A, B, and C -0.1. Nevertheless, we chose C because it is the closest location to our goal. In other words, if you choose C, then the rewards you can get next are much larger than when A and B are selected.

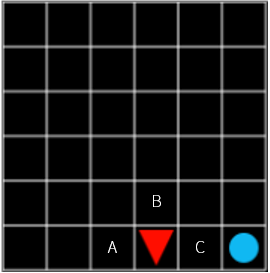Figure 9

Does C in Figure 8 and C in Figure 9 have the same value? How about this?

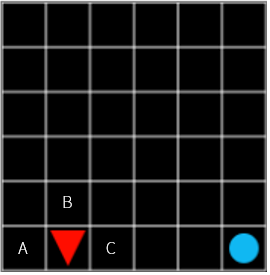Figure 10

Does C in Figure 10 have the same high value as C in Figure 8 and 9 above? If everything is stable now, you can say yes to the example Grid World. But what if a bomb explodes every time you step through it? If you reach the road to your goal, what would be the disturbance that gives you a -100 reward? Nevertheless, going to C is the best choice. However, I can not say that the value is higher than the C in Figure 8. C in Figure 8, there is compensation for just one step in front of you, while C in Figure 10 is uncertain.

A discount rate is introduced to account for this. A discount rate is a concept that means that the current compensation is worth more than the compensation you will receive in the future. In other words, future compensation is worth less than the current compensation. It is expressed as a number between 0.0 and 1.0, usually 0.95, 0.99 and so on. In the mathematical expression, it is represented by the symbol \(\gamma\)(gamma).

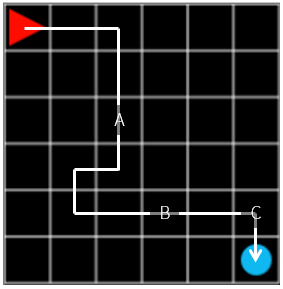Figure 11. steps: 12, reward: -0.1

Applying the discount rate shown above, the highest contribution in A, B, and C in Figure 11 would be C, followed by B, A, and so on. If we calculate the reward by multiplying \(\gamma\) by the step that is farther from the final action, the compensation of C is \(\gamma \times -0.1\), the compensation of B is \(\gamma ^ 3 \times -0.1\) and the compensation of A is \(\gamma ^ 8 \times -0.1\) when the total compensation is -0.1.

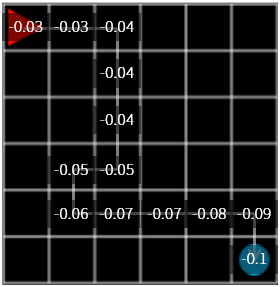Figure 12. Change in reward when \(\gamma = 0.9\)

let canvas = document.getElementById('editor_canvas_2');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
env.maxEpisodes = 50;
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);
env.draw();
agent.draw();

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Loop(random action)';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Run(by reward)';
button2.disabled = true;
canvas.parentNode.appendChild(button2);

let is_running = false;
let rewards_array = [];
let value_array = new Array(env.grid_W * env.grid_W).fill(0);
let cnt_array = new Array(env.grid_W * env.grid_W).fill(0);
let stepped_array;
const gamma = 0.9;

button.onclick = function() {
    if (is_running) return;

    is_running = true;
    stepped_array = [0];
    iterate(true);
}

button2.onclick = function() {
    iterate(true);
}

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    let max = Math.max(...value_array);
    let min = Math.min(...value_array);
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] / max * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor((1.1-Math.abs((value_array[i]-min) / (max-min+1e-4))) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function iterate(is_loop = true) {
    let action;
    if (button2.disabled) {
        action = Math.floor(Math.random() * 4);
    }
    else {
        let values = [];
        let x, y, idx;
        for (let i = 0; i < dirs.length; i += 1) {
            x = agent.x + dirs[i][0];
            y = agent.y + dirs[i][1];
            if (x >= 0 && x < env.width &&
                y >= 0 && y < env.height) {
                idx = x + y * env.grid_W;
                values.push(value_array[idx]);
            }
            else {
                values.push(-Number.MAX_VALUE);
            }
        }

        // find max values
        const m = Math.max(...values);
        values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
        action = values[Math.floor(Math.random() * values.length)];
    }
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();

    let idx = agent.x + agent.y * env.grid_W;
    if (stepped_array.indexOf(idx) === -1) {
        stepped_array.push(idx);
    }

    if (done || env.steps >= env.maxSteps) {
        let reward = Math.floor(agent.reward * 10) / 10;
        rewards_array.push(reward);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 60);
        }

        if (button2.disabled) {
            for (let i = 0; i < stepped_array.length; i += 1) {
                const idx = stepped_array[i];
                cnt_array[idx] += 1;
                value_array[idx] += (reward * (gamma ** (stepped_array.length - i)) - value_array[idx]) / cnt_array[idx];
                value_array[idx] = Math.floor(value_array[idx] * 10) / 10;
            }

            stepped_array = [];
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
    else {
        if (button2.disabled) {
            button2.disabled = false;
            button.disabled = true;
            env.episodes = 0;
        }
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';
});

If you update the reward using \(\gamma = 0.9\), the value change is more pronounced than the above execution. But when we run it, we still have a high percentage of agent wandering away from our goal.

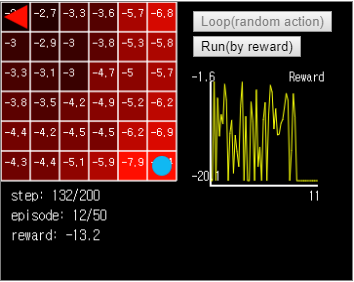Figure 13. When executed in this state, the agent walks endlessly between (x = 0, y = 0) and (x = 1, y = 0).

How do we eliminate this uncertainty? Calculating the Value Function, the title of today’s article, can eliminate the uncertainty and send the agent to the target very quickly.

Value Function

We can solve this problem by getting the value function for each state and moving it to the most valuable state. A value function is a numerical representation of the value of a state. In the picture below, in the case of a Tic-tac-toe game, we can see that the middle column has the highest value of 0.7 without placing anything on the game board.

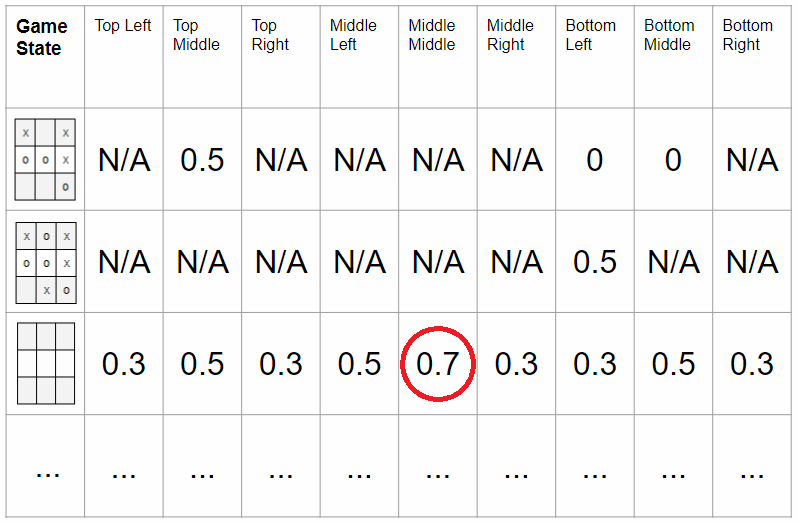Figure 14. In the Tic-tac-toe game, the middle column of the middle line is the most valuable when starting. Source link

Let’s calculate the value function using \(\gamma\). We will use \(\gamma=0.9\).

The value function is initially set to zero for all states. However, since the target grid is in a state in which the Episode ends when it reaches it, the value function is fixed with the same value as the compensation. That is, the value of the target grid is +1.

let canvas = document.getElementById('editor_canvas_3');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1}, [[5, 5]]);

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Get Value';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Get Value x10';
canvas.parentNode.appendChild(button2);

let button3 = document.createElement('button');
button3.style.position = 'absolute';
button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
button3.width = 350 - env.grid_W * env.grid_width - 30;
button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 20).toString() + 'px';
button3.innerHTML = 'Loop(Value)';
canvas.parentNode.appendChild(button3);

let value_array = new Array(env.grid_W * env.grid_W).fill(0);
value_array[value_array.length - 1] = 1;
const gamma = 0.9;

drawValue();
env.draw();

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor(Math.abs(value_array[i]) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function value_iterate() {
    let new_value_array = value_array.slice();
    let x, y;
    let nx, ny;
    let add_value;
    for (let i = 0; i < value_array.length - 1; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        add_value = -Number.MAX_VALUE;
        for (let j = 0; j < dirs.length; j += 1) {
            nx = x + dirs[j][0];
            ny = y + dirs[j][1];
            if (nx >= 0 && nx < env.width &&
                ny >= 0 && ny < env.height) {
                add_value = Math.max(add_value, value_array[nx + ny * env.grid_W] * gamma);
            }
        }

        new_value_array[i] = -0.1 + add_value;
        new_value_array[i] = Math.floor(new_value_array[i] * 100) / 100;
    }
    value_array = new_value_array;
}

button.onclick = function() {
    value_iterate();
    drawValue();
}

button2.onclick = function() {
    for (let i = 0; i < 10; i += 1) {
        value_iterate();
    }
    drawValue();
}

let is_running = false;
let rewards_array = [];

button3.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let values = [];
    let x, y, idx;
    for (let i = 0; i < dirs.length; i += 1) {
        x = agent.x + dirs[i][0];
        y = agent.y + dirs[i][1];
        if (x >= 0 && x < env.width &&
            y >= 0 && y < env.height) {
            idx = x + y * env.grid_W;
            values.push(value_array[idx]);
        }
        else {
            values.push(-Number.MAX_VALUE);
        }
    }

    // find max values
    const m = Math.max(...values);
    values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
    let action = values[Math.floor(Math.random() * values.length)];
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 80);
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';

    button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
    button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 50).toString() + 'px';
});

At this time, the value of a certain grid can be calculated by the following formula.

\[V_{grid} = -0.1 + max(\gamma \times V_{neighbor grid})\]

If it is not the target grid, add -0.1 because you get a reward of -0.1 no matter where you move. It is assumed that it moves to the grid with the greatest value function among neighboring grids, and the max value of the value function of the neighboring grid is added.

Press the Get Value button on the right side to calculate the value once and update the value. You can see that the values are newly calculated from the two grids (x = 5, y = 4), (x = 4, y = 5) around the target. If you press Get Value multiple times, the value is updated chained to the starting point, but after the value is fixed, there is no further change.

When the Loop (Value) button is pressed, the agent compares the value of the neighboring grid of the currently located grid and moves it to the grid with the higher value. If all the grids have the same value, they move to a random position. If the entire Grid World value function is calculated, the agent immediately finds the optimal path.

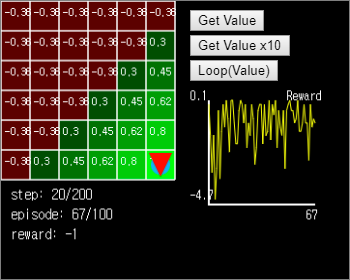Figure 15. In the green area where the value is calculated, the agent immediately finds the optimal path.

Why do not you add a pit that gets a penalty if the agent is missing?

let canvas = document.getElementById('editor_canvas_4');
let ctx = canvas.getContext('2d');
let env = new Env(6, canvas);
let agent = new Agent(env, 0, 0, canvas);
agent.ball_count = 1;
env.setEntity(agent, {'ball': 1, 'box': 3}, [[5, 5], [3, 3], [2, 4], [1, 5]]);

const post = document.getElementsByClassName('post')[0];
let button = document.createElement('button');
button.style.position = 'absolute';
button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
button.width = 350 - env.grid_W * env.grid_width - 30;
button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 20).toString() + 'px';
button.innerHTML = 'Get Value';
canvas.parentNode.appendChild(button);

let button2 = document.createElement('button');
button2.style.position = 'absolute';
button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
button2.width = 350 - env.grid_W * env.grid_width - 30;
button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 20).toString() + 'px';
button2.innerHTML = 'Get Value x10';
canvas.parentNode.appendChild(button2);

let button3 = document.createElement('button');
button3.style.position = 'absolute';
button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
button3.width = 350 - env.grid_W * env.grid_width - 30;
button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 20).toString() + 'px';
button3.innerHTML = 'Loop(Value)';
canvas.parentNode.appendChild(button3);

let value_array = new Array(env.grid_W * env.grid_W).fill(0);
let initial_value_obj = {};
for (let y = 0; y < env.height; y++) {
    for (let x = 0; x < env.width; x++) {
        if (env.grid[y][x].length !== 0) {
            value_array[x + y * env.grid_W] = env.grid[y][x][0].reward;
            initial_value_obj[(x + y * env.grid_W).toString()] = env.grid[y][x][0].reward;
        }
    }
}
const gamma = 0.9;

drawValue();
env.draw();

function drawValue() {
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    let x, y;
    for (let i = 0; i < value_array.length; i += 1) {
        ctx.beginPath();
        if (value_array[i] >= 0) {
            ctx.fillStyle = `rgb(0, ${Math.floor(value_array[i] * 255)}, 0)`;
        }
        else {
            ctx.fillStyle = `rgb(${Math.floor(Math.abs(value_array[i]) * 255)}, 0, 0)`;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillRect(x * env.grid_width, y * env.grid_width, env.grid_width, env.grid_width);
        ctx.closePath();
    }

    ctx.beginPath();
    ctx.fillStyle = 'white';
    ctx.font = '11px monospace';
    for (let i = 0; i < value_array.length; i += 1) {
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        ctx.fillText(value_array[i], (x+0.1) * env.grid_width, (y+0.5) * env.grid_width);
    }
    ctx.closePath();

    env.drawOutline();
}

function value_iterate() {
    let new_value_array = value_array.slice();
    let x, y;
    let nx, ny;
    let add_value;
    for (let i = 0; i < value_array.length; i += 1) {
        if (initial_value_obj.hasOwnProperty(i.toString())) {
            new_value_array[i] = initial_value_obj[i.toString()];
            continue;
        }
        x = i % env.grid_W;
        y = Math.floor(i / env.grid_W);
        add_value = -Number.MAX_VALUE;
        for (let j = 0; j < dirs.length; j += 1) {
            nx = x + dirs[j][0];
            ny = y + dirs[j][1];
            if (nx >= 0 && nx < env.width &&
                ny >= 0 && ny < env.height) {
                add_value = Math.max(add_value, value_array[nx + ny * env.grid_W] * gamma);
            }
        }

        new_value_array[i] = -0.1 + add_value;
        new_value_array[i] = Math.floor(new_value_array[i] * 100) / 100;
    }
    value_array = new_value_array;
}

button.onclick = function() {
    value_iterate();
    drawValue();
}

button2.onclick = function() {
    for (let i = 0; i < 10; i += 1) {
        value_iterate();
    }
    drawValue();
}

let is_running = false;
let rewards_array = [];

button3.onclick = function() {
    if (is_running) return;
    is_running = true;
    iterate(true);
}

function iterate(is_loop = true) {
    let values = [];
    let x, y, idx;
    for (let i = 0; i < dirs.length; i += 1) {
        x = agent.x + dirs[i][0];
        y = agent.y + dirs[i][1];
        if (x >= 0 && x < env.width &&
            y >= 0 && y < env.height) {
            idx = x + y * env.grid_W;
            values.push(value_array[idx]);
        }
        else {
            values.push(-Number.MAX_VALUE);
        }
    }

    // find max values
    const m = Math.max(...values);
    values = values.map((c,i) => c == m ? i : -1).filter(c => c >= 0);
    let action = values[Math.floor(Math.random() * values.length)];
    let reward, done;
    [reward, done] = agent.step(action);
    agent.reward += reward;
    agent.reward = parseFloat((agent.reward).toFixed(2));
    ctx.clearRect(0, 0, env.grid_W * env.grid_width + 10, canvas.height);

    env.steps += 1;
    drawValue();
    env.draw();
    agent.draw();


    if (done || env.steps >= env.maxSteps) {
        rewards_array.push(Math.floor(agent.reward * 10) / 10);
        if (rewards_array.length > 1) {
            ctx.clearRect(env.grid_W * env.grid_width + 10, 0, canvas.width, canvas.height);
            env.drawRewardGraph(rewards_array, 195, 80);
        }

        agent.x = 0;
        agent.y = 0;
        agent.reward = 0;
        agent.dir = 3;
        agent.ball_count = 1;

        env.episodes += 1;
        env.steps = 0;
        env.reset();

        while (true) {
            if (env.setEntity(agent, {'ball': 1}, [[5, 5]]) !== null) {
                break;
            }
        }
    }
    if (is_loop && env.episodes < env.maxEpisodes) {
        window.requestAnimationFrame(iterate);
    }
}

window.addEventListener('resize', function() {
    button.style.top = (canvas.parentNode.offsetTop + 10).toString() + 'px';
    button.style.left = (post.offsetLeft + post.offsetWidth - button.width - 30).toString() + 'px';

    button2.style.top = (canvas.parentNode.offsetTop + 35).toString() + 'px';
    button2.style.left = (post.offsetLeft + post.offsetWidth - button2.width - 30).toString() + 'px';

    button3.style.top = (canvas.parentNode.offsetTop + 60).toString() + 'px';
    button3.style.left = (post.offsetLeft + post.offsetWidth - button3.width - 50).toString() + 'px';
});

I have placed a yellow square at three locations: (x = 1, y = 5), (x = 2, y = 4), and (x = 3, y = 3). When agent reach here, the agent receives -1.

If you click the Get Value button to update the value function for each state, you can see that the yellow square is fixed at -1 and does not update according to the convention set above. If you update the value function by pressing multiple times, you can see that the value function is slow to reach the bottom left of Grid World. If you move the agent by pressing the Loop (Value) button, you can move to the upper right path to avoid reaching the goal by avoiding the blocked section.

We have studied Grid World, one of the basic environments of reinforcement learning, and the calculation and use of the value function, which is one of the basic algorithms. Next time I’ll come up with some more challenging problems and suggest more efficient algorithms to solve them. Thank you for reading the long article.

The style of Grid World refers to the gym-minigrid of Maxime Chevalier-Boisvert. ↩

greentec's blog game designer, scripter, researcher

Learn Reinforcement Learning (1) - Value Function

What is reinforcement learning?

Theoretical background

Grid World

Value Function

Related Posts

Creating a Queens game map on Linkedin 13 May 2024

CoG 2019 attendance review 29 Aug 2019

Learn Reinforcement Learning (5) - Solving problems with a door and a key 09 Jun 2019